Advertisements
Advertisements
Question
Write the co-ordinates of the point of intersection of graphs of
equations x = 2 and y = -3.
Solution
The co-ordinates of point of intersection of x = 2 and y = -3 are (2,-3).
APPEARS IN
RELATED QUESTIONS
A(5, 3), B(–1, 1) and C(7, –3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show that : `LM = 1/2 BC`.
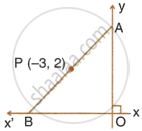
P(–3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.
One end of the diameter of a circle is (–2, 5). Find the co-ordinates of the other end of it, if the centre of the circle is (2, –1).
The points (2, –1), (–1, 4) and (–2, 2) are mid-points of the sides of a triangle. Find its vertices.
Points A(–5, x), B(y, 7) and C(1, –3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.
Three consecutive vertices of a parallelogram ABCD are A(S, 5), B(-7, -5) and C(-5, 5). Find the coordinates of the fourth vertex D.
Find the length of the median through the vertex A of triangle ABC whose vertices are A (7, -3), B(S, 3) and C(3, -1).
A triangle is formed by line segments joining the points (5, 1 ), (3, 4) and (1, 1). Find the coordinates of the centroid.
The midpoints of three sides of a triangle are (1, 2), (2, -3) and (3, 4). Find the centroid of the triangle.
ABC is a triangle whose vertices are A(-4, 2), B(O, 2) and C(-2, -4). D. E and Fare the midpoint of the sides BC, CA and AB respectively. Prove that the centroid of the Δ ABC coincides with the centroid of the Δ DEF.
If P(–b, 9a – 2) divides the line segment joining the points A(–3, 3a + 1) and B(5, 8a) in the ratio 3: 1, find the values of a and b.
Point M is the mid-point of segment AB. If AB = 8.6 cm, then find AM.
The mid-point of the sides of a triangle are (2, 4), (−2, 3) and (5, 2). Find the coordinates of the vertices of the triangle
The points A(−5, 4), B(−1, −2) and C(5, 2) are the vertices of an isosceles right-angled triangle where the right angle is at B. Find the coordinates of D so that ABCD is a square
A(−3, 2), B(3, 2) and C(−3, −2) are the vertices of the right triangle, right angled at A. Show that the mid-point of the hypotenuse is equidistant from the vertices
In what ratio does the point Q(1, 6) divide the line segment joining the points P(2, 7) and R(−2, 3)
Find the co-ordinates of centroid of a triangle if points D(–7, 6), E(8, 5) and F(2, –2) are the mid-points of the sides of that triangle.
