Question

The points (2, –1), (–1, 4) and (–2, 2) are mid-points of the sides of a triangle. Find its vertices.

Answer 1

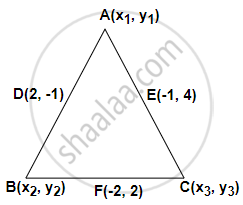
Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the coordinates of the vertices of ΔABC.

Midpoint of AB, i.e. D

`D(2, -1) = D((x_1 + x_2)/2, (y_1 + y_2)/2)`

`2 = (x_1 + x_2)/2, (y_1 + y_2)/2 = -1`

x₁ + x₂ = 4   ...(1)

y₁ + y₂ = –2  ...(2)

Similarly

x₁ + x₂ = –2   ...(3)

y₁ + y₃ =  8   ...(4)

x₁ + x₃ = −4   ...(5)

y₂ + y₃ =  4   ...(6)

Adding (1), (3) and (5), we get,

2(x₁ + x₂ + x₃) = –2

x₁ + x₂ + x₃ = –1

4 + x₃ = –1  ...[From (1)]

x₃ = –5 

From (3)

x₁ – 5 = –2

x₁ = 3

From (5)

x₂ – 5 = –4

x₂ = 1

Adding (2), (4) and (6), we get,

2(y₁ + y₂ + y₃) = 10

y₁ + y₂ + y₃ = 5

–2 + y₃ = 5  ...[From (2)]

y₃ = 7

From (4)

y₁ + 7 = 8

y₁ = 1

From (6)

y₂ + 7 = 4

y₂ = –3

Thus, the co-ordinates of the vertices of ΔABC are (3, 1), (1, –3) and (–5, 7).