Advertisements
Advertisements
प्रश्न
Write the co-ordinates of the point of intersection of graphs of
equations x = 2 and y = -3.
उत्तर
The co-ordinates of point of intersection of x = 2 and y = -3 are (2,-3).
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). Find
1) Coordinates of A
2) An equation of diagonal BD
Find the mid-point of the line segment joining the points:
(–6, 7) and (3, 5)
(–5, 2), (3, −6) and (7, 4) are the vertices of a triangle. Find the length of its median through the vertex (3, −6).
Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
Points P(a, −4), Q(−2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
The co-ordinates of the centroid of a triangle PQR are (2, –5). If Q = (–6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.
If the midpoints of the sides ofa triangle are (-2, 3), (4, -3), (4, 5), find its vertices.
Find the centroid of a triangle whose vertices are (3, -5), (-7, 4) and ( 10, -2).
A( 4, 2), B(-2, -6) and C(l, 1) are the vertices of triangle ABC. Find its centroid and the length of the median through C.
A triangle is formed by line segments joining the points (5, 1 ), (3, 4) and (1, 1). Find the coordinates of the centroid.
A , B and C are collinear points such that AB = `1/2` AC . If the coordinates of A, B and C are (-4 , -4) , (-2 , b) anf (a , 2),Find the values of a and b.
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
The mid-point of the sides of a triangle are (2, 4), (−2, 3) and (5, 2). Find the coordinates of the vertices of the triangle
In what ratio does the point Q(1, 6) divide the line segment joining the points P(2, 7) and R(−2, 3)
If the coordinates of one end of a diameter of a circle is (3, 4) and the coordinates of its centre is (−3, 2), then the coordinate of the other end of the diameter is
The ratio in which the x-axis divides the line segment joining the points (6, 4) and (1, −7) is
Point P is midpoint of segment AB where A(– 4, 2) and B(6, 2), then the coordinates of P are ______
From the figure given alongside, find the length of the median AD of triangle ABC. Complete the activity.
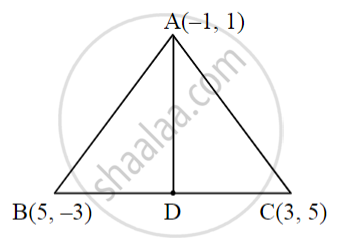
Solution:
Here A(–1, 1), B(5, – 3), C(3, 5) and suppose D(x, y) are coordinates of point D.
Using midpoint formula,
x = `(5 + 3)/2`
∴ x = `square`
y = `(-3 + 5)/2`
∴ y = `square`
Using distance formula,
∴ AD = `sqrt((4 - square)^2 + (1 - 1)^2`
∴ AD = `sqrt((square)^2 + (0)^2`
∴ AD = `sqrt(square)`
∴ The length of median AD = `square`
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the coordinates of D.
