Advertisements
Advertisements
Question
Given M is the mid-point of AB, find the co-ordinates of B; if A = (3, –1) and M = (–1, 3).
Solution
Let B = (x, y), M = (–1, 3), A = (3, –1)
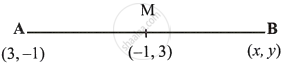
∴ `-1 = (x + 3)/2`
`=>` x + 3 = –2
∴ x = –2 – 3 = –5
`3 = (y - 1)/2`
`=>` y – 1 = 6
∴ y = 6 + 1 = 7
∴ Co-ordinates of B are (–5, 7)
APPEARS IN
RELATED QUESTIONS
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
Find the midpoint of the line segment joining the following pair of point :
( -3, 5) and (9, -9)
Find the midpoint of the line segment joining the following pair of point :
(3a-2b, Sa+7b) and (a+4b, a-3b)
(4, 2) and (-1, 5) are the adjacent vertices ofa parallelogram. (-3, 2) are the coordinates of the points of intersection of its diagonals. Find the coordinates of the other two vertices.
If (-3, 2), (1, -2) and (5, 6) are the midpoints of the sides of a triangle, find the coordinates of the vertices of the triangle.
A lies on the x - axis amd B lies on the y -axis . The midpoint of the line segment AB is (4 , -3). Find the coordinates of A and B .
The mid-point of the line joining (−a, 2b) and (−3a, −4b) is
If A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a ∆ABC. Segment AD is median. Find the length of seg AD:
Point M (2, b) is the mid-point of the line segment joining points P (a, 7) and Q (6, 5). Find the values of ‘a’ and ‘b’.
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the coordinates of D.
