Advertisements
Advertisements
Question
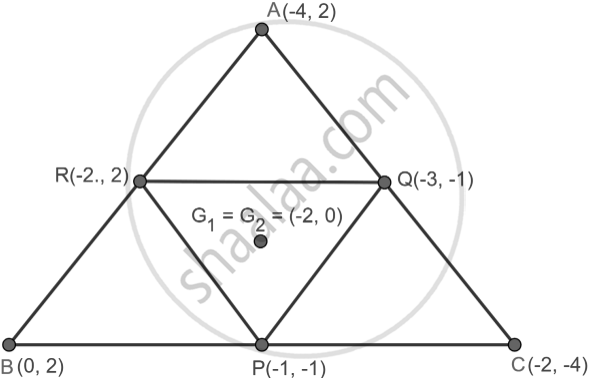
A(–4, 2), B(0, 2) and C(–2, –4) are vertices of a triangle ABC. P, Q and R are mid-points of sides BC, CA and AB respectively. Show that the centroid of ΔPQR is the same as the centroid of ΔABC.
Solution
By formula,
Mid-point (M) =`((x_1 + x_2)/2, (y_1 + y_2)/2)`
Given:
P is mid-point of BC.
∴ `P = ((0 + (-2))/2, (2 + (-4))/2)`
= `(-2/2, -2/2)`
= (–1, –1)
Q is mid-point of CA.
∴ `Q = ((-2 + (-4))/2, (-4 + 2)/2)`
= `(-6/2, -2/2)`
= (–3, –1)
R is mid-point of AB.
∴ `R = ((-4 + 0)/2, (2 + 2)/2)`
= `(-4/2, 4/2)`
= (–2, 2)
Centroid of the triangle is given by (G)
= `((x_2 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`
Let G1 and G2 be the centroid of △ABC and △PQR.
Substituting values we get,
`G_1 = ((-4 + 0 + (-2))/3, (2 + 2 + (-4))/3)`
= `(-6/3 , 0/3)`
= (–2, 0)
`G_2 = (((-1) + (-3) + (-2))/3, ((-1) + (-1) + 2)/3)`
= `(-6/3 , 0/3)`
= (–2, 0)
Since, G1 = G2.
Hence, proved that the centroid of △PQR is the same as the centroid of △ABC.
APPEARS IN
RELATED QUESTIONS
P(1, -2) is a point on the line segment A(3, -6) and B(x, y) such that AP : PB is equal to 2 : 3. Find the coordinates of B.
Calculate the co-ordinates of the point P which divides the line segment joining: A (–4, 6) and B (3, –5) in the ratio 3 : 2
Find the image of the point A(5, –3) under reflection in the point P(–1, 3).
Find the image of the point A(5,3) under reflection in the point P(-1,3).
Find the image of the point A(5,3) under reflection in the point P(-1,3).
Find the image of the point A(5,3) under reflection in the point P(-1,3).
Prove that the points A(-5, 4), B(-1, -2) and C(S, 2) are the vertices of an isosceles right-angled triangle. Find the coordinates of D so that ABCD is a square.
In the following figure line APB meets the X-axis at A, Y-axis at B. P is the point (4, -2) and AP: PB = 1: 2. Write down the coordinates of A and B.
Determine the centre of the circle on which the points (1, 7), (7 – 1), and (8, 6) lie. What is the radius of the circle?
From the adjacent figure:
(i) Write the coordinates of the points A, B, and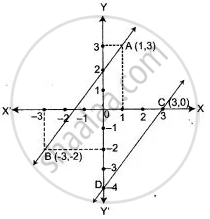
(ii) Write the slope of the line AB.
(iii) Line through C, drawn parallel to AB, intersects Y-axis at D. Calculate the co-ordinates of D.
