Advertisements
Advertisements
Question
Determine the centre of the circle on which the points (1, 7), (7 – 1), and (8, 6) lie. What is the radius of the circle?
Solution
Let P(x, y) be the centre of the circle and A(1, 7), B(7, -1) and C(8, 6) be the given points.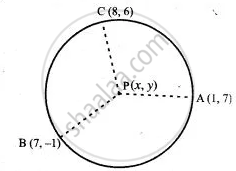
Then PA = PB = PC = radius
⇒ PA2 = PB = PC = r2
⇒ (x - 1)2 + y( - 7)2 = r2 ...(i)
(x - 7)2 + (y + 1)2 = r2 ...(ii)
Also (x - 8)2 + (y - 6)2 = r2 ...(iii)
Subtracting (ii) from (i)
(x2 + 1 - 2x + y2 + 49 - 14y)
-(x2 + 49 - 14x + y2 + 1 + 2y) = 0
⇒ 12x - 16y = 0
`y = (3)/(4)x` ...(iv)
Subtracting (iii) from (ii)
⇒ (x2 + 49 - 14x + y2 + 1 + 2y)
-(x2 + 64 - 16x + y2 + 36 - 12y) = 0
⇒ 2x + 14y - 50 = 0
⇒ `x + 7(3/4x)-25` = 0
⇒ `(25x)/(4)` = 25
⇒ x = 4
From (iv) y = `(3)/(4)x = (3)/(4) xx 4`
y = 3.
The centre is P(4, 3).
Also radius, r = PA = `sqrt((4 - 1)^2 + (3 - 7)^2)`
= `sqrt(9 + 16)`
= 5 units.
APPEARS IN
RELATED QUESTIONS
P(1, -2) is a point on the line segment A(3, -6) and B(x, y) such that AP : PB is equal to 2 : 3. Find the coordinates of B.
Calculate the ratio in which the line joining A(-4,2) and B(3,6) is divided by point p(x,3). Also, find x
If the abscissa of a point P is 2, find the ratio in which this point divides the line segment joining the point (−4, 3) and (6, 3). Also, find the co-ordinates of point P.
The line joining the points (2, 1) and (5, –8) is trisected at the point P and Q. If point P lies on the line 2x – y + k = 0, find the value of k. Also, find the co-ordinates of point Q.
M is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1 : 3. Find :
- co-ordinates of M
- co-ordinates of P
- length of BP

Find the image of the point A(5,3) under reflection in the point P(-1,3).
Find the image of the point A(5,3) under reflection in the point P(-1,3).
The line segment joining A (2, 3) and B (6, – 5) is intersected by the X axis at the point K. Write the ordinate of the point K. Hence find the ratio in which K divides AB.
If the line joining the points A(4, - 5) and B(4, 5) is divided by the point P such that `"AP"/"AB" = (2)/(5)`, find the coordinates of P.
From the adjacent figure:
(i) Write the coordinates of the points A, B, and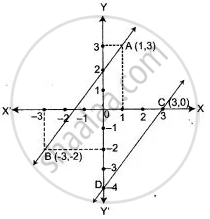
(ii) Write the slope of the line AB.
(iii) Line through C, drawn parallel to AB, intersects Y-axis at D. Calculate the co-ordinates of D.
