Advertisements
Advertisements
Question
Find the image of a point (-1, 2) in the line joining (2, 1) and (- 3, 2).
Solution
Let D(α, β) be the image of point C(-1, 2) in the line joining the points A(2, 1) and B(-3, 2).
Since AB is the perpendicular bisector of CD.
So, Slope of AB x Slope of CD = -1
⇒ `(2 - 1)/(-3 -2) xx (beta - 2)/(α + 1)` = -1
⇒ `(1)/(-5) xx (beta - 2)/(α + 1)` = -1
⇒ β - 2 = 5α + 5
⇒ 5α - β + 7 = 0 ...(i)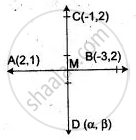
Equation of line AB,
y - 1 = `(2 - 1)/(-3 - 2)(x - 2)`
⇒ y - 1 = `(1)/(-5)(x - 2)`
⇒ -5(y - 1) = x - 2
⇒ x - 2 + 5y - 5 = 0
⇒ x + 5y - 7 = 0 ...(ii)
Since, midpoint of CD `((α - 1)/2,(beta + 2)/2)`lies on AB.
`(α - 1)/(2) + 5 ((beta + 2)/2) -7` = 0
⇒ α - 1 + 5β + 10 - 14 = 0
⇒ α + 5β - 5 = 0 ...(iii)
Solving (i) and (iii), we get
α = `(-15)/(13) and beta = (16)/(13)`
Hence, coordination of D are `(-15/13,16/13)`.
APPEARS IN
RELATED QUESTIONS
Find the slope of the line perpendicular to AB if : A = (3, −2) and B = (−1, 2)
Find the slope and the inclination of the line AB if : A = `(0, - sqrt(3))` and B = (3, 0)
Angles made by the line with the positive direction of X–axis is given. Find the slope of these line.
90°
Find the slope of the lines passing through the given point.
P (–3, 1) , Q (5, –2)
Fill in the blank using correct alternative.
Out of the following, point ........ lies to the right of the origin on X– axis.
Determine whether the given point is collinear.
A (0, 2), B (1, -0.5), C (2, -3)
Find the slope of a line, correct of two decimals, whose inclination is 60°
Find the slope of a line passing through the given pair of points (9,-2) and (-5,5)
Find the slope of a line passing through the following pair of point
(²m²,2am) and (p²m²,2pm)
