Advertisements
Advertisements
प्रश्न
Find the image of a point (-1, 2) in the line joining (2, 1) and (- 3, 2).
उत्तर
Let D(α, β) be the image of point C(-1, 2) in the line joining the points A(2, 1) and B(-3, 2).
Since AB is the perpendicular bisector of CD.
So, Slope of AB x Slope of CD = -1
⇒ `(2 - 1)/(-3 -2) xx (beta - 2)/(α + 1)` = -1
⇒ `(1)/(-5) xx (beta - 2)/(α + 1)` = -1
⇒ β - 2 = 5α + 5
⇒ 5α - β + 7 = 0 ...(i)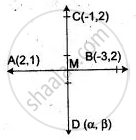
Equation of line AB,
y - 1 = `(2 - 1)/(-3 - 2)(x - 2)`
⇒ y - 1 = `(1)/(-5)(x - 2)`
⇒ -5(y - 1) = x - 2
⇒ x - 2 + 5y - 5 = 0
⇒ x + 5y - 7 = 0 ...(ii)
Since, midpoint of CD `((α - 1)/2,(beta + 2)/2)`lies on AB.
`(α - 1)/(2) + 5 ((beta + 2)/2) -7` = 0
⇒ α - 1 + 5β + 10 - 14 = 0
⇒ α + 5β - 5 = 0 ...(iii)
Solving (i) and (iii), we get
α = `(-15)/(13) and beta = (16)/(13)`
Hence, coordination of D are `(-15/13,16/13)`.
APPEARS IN
संबंधित प्रश्न
Find the slope of the line passing through the points A(-2, 1) and B(0, 3).
Find the slope of the line parallel to AB if : A = (−2, 4) and B = (0, 6)
The side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides. Also, find:
- the slope of the diagonal AC.
- the slope of the diagonal BD.
Find the slope of the line which is parallel to x + 2y + 3 = 0
Find the type of the quadrilateral if points A(–4, –2), B(–3, –7) C(3, –2) and D(2, 3) are joined serially.
Find the slope of a line, correct of two decimals, whose inclination is 30°
Find the slope of a line passing through the following pair of point
(²m²,2am) and (p²m²,2pm)
Find the slope of a line passing through the following pair of points
(5pq,p2q) and (5qr,qr2)
If the lines 7y = ax + 4 and 2y = 3 − x, are parallel to each other, then the value of ‘a’ is:
