Advertisements
Advertisements
प्रश्न
Find the slope of the line which is parallel to x + 2y + 3 = 0
उत्तर
x + 2y + 3 = 0
2y = −x − 3
`y = (-1)/2x -3/2`
Slope of this line = `(-1)/2`
Slope of the line which is parallel to the given line = Slope of the given line = `(-1)/2`
APPEARS IN
संबंधित प्रश्न
A slope of a line is 3 and y-intercept is –4. Write the equation of a line
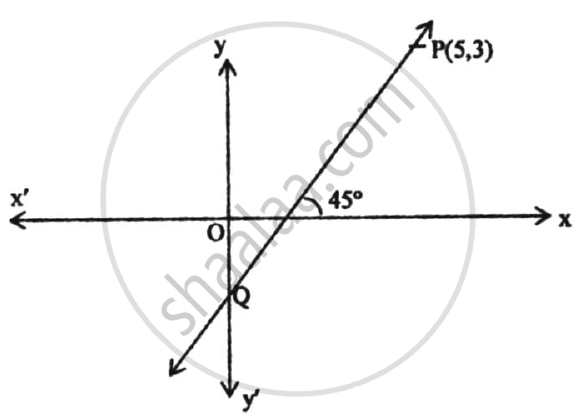
The line through P(5, 3) intersects y-axis at Q.
(1) Write the slope of the line.
(2) Write the equation of the line.
(3) Find the coordinates of Q.
Find the slope of the line perpendicular to AB if : A = (0, −5) and B = (−2, 4)
Plot the points A(1, 1), B(4, 7) and C(4, 10) on a graph paper. Connect A and B and also A and C.
Which segment appears to have the steeper slope, AB or AC?
Justify your conclusion by calculating the slopes of AB and AC.
Find the slope of the line which is perpendicular to `x/3 - 2y = 4`
Find the slope of a line passing through the given pair of points (-5,-1) and (-9,-7)
Find the slope and the y-intercept of the following line 3x + y = 7
Find the slope of the line passing through the points A(6, -2) and B(–3, 4).
Show that points A(– 4, –7), B(–1, 2), C(8, 5) and D(5, – 4) are the vertices of a parallelogram ABCD
Determine whether the following points are collinear. A(–1, –1), B(0, 1), C(1, 3)
Given: Points A(–1, –1), B(0, 1) and C(1, 3)
Slope of line AB = `(square - square)/(square - square) = square/square` = 2
Slope of line BC = `(square - square)/(square - square) = square/square` = 2
Slope of line AB = Slope of line BC and B is the common point.
∴ Points A, B and C are collinear.
