Advertisements
Advertisements
प्रश्न
Plot the points A(1, 1), B(4, 7) and C(4, 10) on a graph paper. Connect A and B and also A and C.
Which segment appears to have the steeper slope, AB or AC?
Justify your conclusion by calculating the slopes of AB and AC.
उत्तर

From the graph, clearly, AC has steeper slope.
Slope of AB = `(7 - 1)/(4 - 1) = 6/3 = 2`
Slope of AC = `(10 - 1)/(4 - 1) = 9/3 = 3`
The line with greater slope is steeper.
Hence, AC has steeper slope.
APPEARS IN
संबंधित प्रश्न
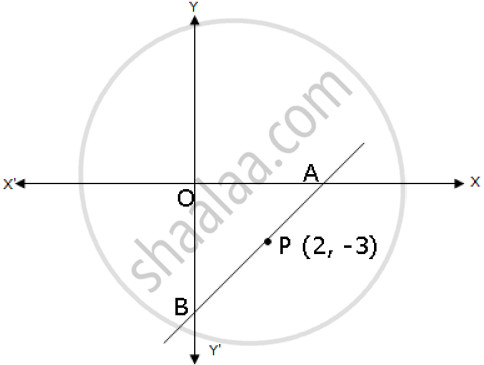
A and B are two points on the x-axis and y-axis respectively. P (2, −3) is the midpoint of AB. Find the:
(1) coordinates of A and B
(2) slope of line AB.
(3) an equation of line AB.
Find the value(s) of k so that PQ will be parallel to RS. Given : P(2, 4), Q(3, 6), R(8, 1) and S(10, k)
Find the slope of the lines passing through the given point.
L (–2, –3) , M (–6, –8)
If A(1, –1), B(0, 4), C(–5, 3) are vertices of a triangle then find the slope of each side.
Show that points P(1, –2), Q(5, 2), R(3, –1), S(–1, –5) are the vertices of a parallelogram.
Find the slope of a line passing through the given pair of points (0,5) and (5,0)
Find the slope of the line passing through the points M(4,0) and N(-2,-3).
With out Pythagoras theorem, show that A(4, 4), B(3, 5) and C(-1, -1) are the vertices of a right angled.
Find the image of a point (-1, 2) in the line joining (2, 1) and (- 3, 2).
Determine whether the following points are collinear. A(–1, –1), B(0, 1), C(1, 3)
Given: Points A(–1, –1), B(0, 1) and C(1, 3)
Slope of line AB = `(square - square)/(square - square) = square/square` = 2
Slope of line BC = `(square - square)/(square - square) = square/square` = 2
Slope of line AB = Slope of line BC and B is the common point.
∴ Points A, B and C are collinear.
