Advertisements
Advertisements
प्रश्न
If A(1, –1), B(0, 4), C(–5, 3) are vertices of a triangle then find the slope of each side.
उत्तर
A (1, –1), B (0, 4), C (–5, 3) form a triangle.
\[\text{We know that, slope of line}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
Slope of AB = \[\frac{4 - \left( - 1 \right)}{0 - 1} = \frac{5}{- 1} = - 5\]
Slope of BC = \[\frac{3 - 4}{- 5 - 0} = \frac{- 1}{- 5} = \frac{1}{5}\]
Slope of AC = \[\frac{3 - \left( - 1 \right)}{- 5 - 1} = \frac{4}{- 6} = \frac{- 2}{3}\]
∴ The slopes of the sides AB, BC and AC are -5, \[\frac{1}{5}\] and \[\frac{-2}3\] respectively.
APPEARS IN
संबंधित प्रश्न
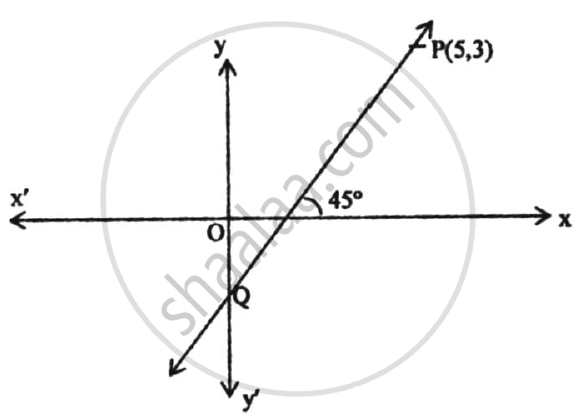
The line through P(5, 3) intersects y-axis at Q.
(1) Write the slope of the line.
(2) Write the equation of the line.
(3) Find the coordinates of Q.
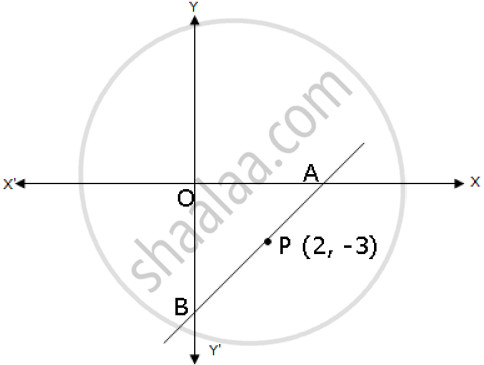
A and B are two points on the x-axis and y-axis respectively. P (2, −3) is the midpoint of AB. Find the:
(1) coordinates of A and B
(2) slope of line AB.
(3) an equation of line AB.
Find the slope of the line parallel to AB if : A = (−2, 4) and B = (0, 6)
Without using the distance formula, show that the points A(4, 5), B(1, 2), C(4, 3) and D(7, 6) are the vertices of a parallelogram.
A(5, 4), B(−3, −2) and C(1, −8) are the vertices of a triangle ABC. Find:
- the slope of the altitude of AB,
- the slope of the median AD and
- the slope of the line parallel to AC.
The points (−3, 2), (2, −1) and (a, 4) are collinear. Find a.
Find the slope of the line which is perpendicular to `x - y/2 + 3 = 0`
If the lines y = 3x + 7 and 2y + px = 3 are perpendicular to each other, find the value of p.
Find the slope of the lines passing through the given point.
L (–2, –3) , M (–6, –8)
Show that A(–4, –7), B (–1, 2), C (8, 5) and D (5, –4) are the vertices of a parallelogram.
Fill in the blank using correct alternative.
A line makes an angle of 30° with the positive direction of X– axis. So the slope of the line is ______.
Find the type of the quadrilateral if points A(–4, –2), B(–3, –7) C(3, –2) and D(2, 3) are joined serially.
Find the slope of a line, correct of two decimals, whose inclination is 50°
Find the slope of a line, correct of two decimals, whose inclination is 75°
Find the slope of a line, correct of two decimals, whose inclination is 30°
Find the slope of a line passing through the given pair of points (2,5) and (-1,8)
Find the slope of a line passing through the given pair of points (-5,-1) and (-9,-7)
Find the slope of a line parallel to the given line 4x-2y = 3
Find slope of a line passing through the points A(3, 1) and B(5, 3).
Find the image of a point (-1, 2) in the line joining (2, 1) and (- 3, 2).
