Advertisements
Advertisements
प्रश्न
A(5, 4), B(−3, −2) and C(1, −8) are the vertices of a triangle ABC. Find:
- the slope of the altitude of AB,
- the slope of the median AD and
- the slope of the line parallel to AC.
उत्तर
Given, A(5, 4), B(−3, −2) and C(1, −8) are the vertices of a triangle ABC.
i. Slope of AB = `(-2 - 4)/(-3 - 5) = (-6)/(-8) = 3/4`
Slope of the altitude of AB = `(-1)/"slope of AB" = (-1)/(3/4) = (-4)/3`
ii. Since, D is the mid-point of BC.
Co-ordinates of point D are `((-3 + 1)/2, (-2 - 8)/2) = (-1, -5)`
Slope of AD = `(-5 - 4)/(-1 - 5) = (-9)/(-6) = 3/2`
iii. Slope of AC = `(-8 - 4)/(1 - 5) = (-12)/(-4) = 3`
Slope of line parallel to AC = Slope of AC = 3
APPEARS IN
संबंधित प्रश्न
Without using the distance formula, show that the points A(4, 5), B(1, 2), C(4, 3) and D(7, 6) are the vertices of a parallelogram.
Show that the points P(a, b + c), Q(b, c + a) and R(c, a + b) are collinear.
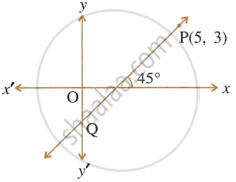
The line through P(5, 3) intersects y-axis at Q.
- Write the slope of the line.
- Write the equation of the line.
- Find the co-ordinates of Q.
The lines represented by 4x + 3y = 9 and px – 6y + 3 = 0 are parallel. Find the value of p.
Find the slope of the lines passing through the given point.
A(2, 3), B(4, 7)
Find the slope of the lines passing through the given point.
P (–3, 1) , Q (5, –2)
Determine whether the following point is collinear.
L(2, 5), M(3, 3), N(5, 1)
Find k if the line passing through points P(–12, –3) and Q(4, k) has slope \[\frac{1}{2}\].
Find the slope of a line, correct of two decimals, whose inclination is 75°
A line passing through the points (a, 2a) and (- 2, 3) is perpendicular to the line 4a + 3y + 5 = 0. Find the value of a.
