Advertisements
Advertisements
प्रश्न
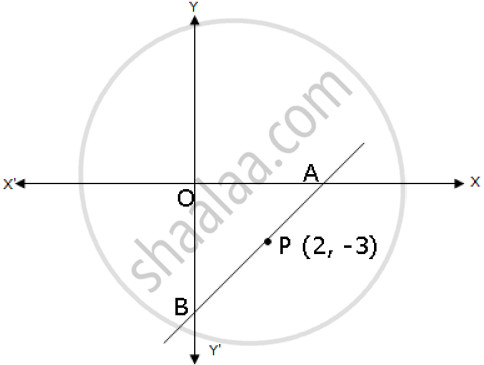
A and B are two points on the x-axis and y-axis respectively. P (2, −3) is the midpoint of AB. Find the:
(1) coordinates of A and B
(2) slope of line AB.
(3) an equation of line AB.
उत्तर
1) Let the coordinates be A(x, 0) and B(0, y).
Mid-point of A and B is given by `((x+0)/2 , (y + 0)/2) = (x/2, y/2)`
`=> (2, -3) = (x/2, y/2)`
=> `x/2 = 2` and `y/2 = -3`
=> x = 4 and y = 6
∴ A(4,0) and B(0,-6)
2) Slope of line AB, m = `(y_2 - y_1)/(x_2 - x_1) = (-6-0)/(0-4) = 3/2`
3) Equation of line AB, using A(4,0)
`y - 0 = 3/2 (x - 4) => 3x - 2y = 12`
APPEARS IN
संबंधित प्रश्न
Show that the points P(a, b + c), Q(b, c + a) and R(c, a + b) are collinear.
Find the value of k for which the lines kx – 5y + 4 = 0 and 5x – 2y + 5 = 0 are perpendicular to each other.
Find the slope of the line passing through the points G(4, 5) and H (–1, –2).
Determine whether the following point is collinear.
D(–2, –3), E(1, 0), F(2, 1)
Find k, if B(k, –5), C (1, 2) and slope of the line is 7.
Fill in the blank using correct alternative.
A line makes an angle of 30° with the positive direction of X– axis. So the slope of the line is ______.
Given that (a, 2a) lies on line`(y)/(2) = 3 - 6`.Find the value of a.
A line passing through the points (a, 2a) and (- 2, 3) is perpendicular to the line 4a + 3y + 5 = 0. Find the value of a.
With out Pythagoras theorem, show that A(4, 4), B(3, 5) and C(-1, -1) are the vertices of a right angled.
Find the image of a point (-1, 2) in the line joining (2, 1) and (- 3, 2).
