Advertisements
Advertisements
Question
The line segment joining A (2, 3) and B (6, – 5) is intersected by the X axis at the point K. Write the ordinate of the point K. Hence find the ratio in which K divides AB.
Solution
A (2, 3) and B (6,- 5)
Intersected at X axis at K.
∴ y = 0 or ordinate = 0
K (x, 0)
Let required ratio be a: 1
∴ Ordinate of K = 0
0 = `(a xx -5 + 1 xx 3)/(a + 1)`
0 = -5a + 3
5a = 3, a = `(3)/(5)`
∴ K divides AB in ratio of 3 : 5.
APPEARS IN
RELATED QUESTIONS
P(1, -2) is a point on the line segment A(3, -6) and B(x, y) such that AP : PB is equal to 2 : 3. Find the coordinates of B.
Calculate the co-ordinates of the point P which divides the line segment joining: A (1, 3) and B (5, 9) in the ratio 1 : 2
Calculate the ratio in which the line joining A(-4,2) and B(3,6) is divided by point p(x,3). Also, find x
Find the ratio in which the line 2x + y = 4 divides the line segment joining the point P(2, –2) and Q(3, 7).
M is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1 : 3. Find :
- co-ordinates of M
- co-ordinates of P
- length of BP

Find the image of the point A(5,3) under reflection in the point P(-1,3).
Find the image of the point A(5,3) under reflection in the point P(-1,3).
Show that the points A(1, 3), B(2, 6), C(5, 7) and D(4, 4) are the vertices of a rhombus.
= `a(1/t^2 + 1) = (a(t^2 + 1))/t^2`
Now `(1)/"SP" + (1)/"SQ" = (1)/(a(t^2 + 1)) + (1 xx t^2)/(a(t^2 + 1)`
= `((1 + t^2))/(a(t^2 + 1)`
`(1)/"SP" + (1)/"SQ" = (1)/a`.
The midpoint of the line segment AB shown in the diagram is (4, – 3). Write down the coordinates of A and B.
From the adjacent figure:
(i) Write the coordinates of the points A, B, and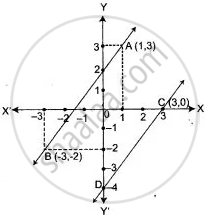
(ii) Write the slope of the line AB.
(iii) Line through C, drawn parallel to AB, intersects Y-axis at D. Calculate the co-ordinates of D.
