Advertisements
Advertisements
Question
Find the mid-point of the line segment joining the points:
(5, –3) and (–1, 7)
Solution
A(5, –3) and B(–1, 7)
Mid-point of AB = `((5 - 1)/2, (-3 + 7)/2)`
= (2, 2)
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). Find
1) Coordinates of A
2) An equation of diagonal BD
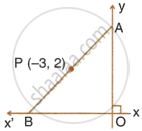
P(–3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.
One end of the diameter of a circle is (–2, 5). Find the co-ordinates of the other end of it, if the centre of the circle is (2, –1).
The mid-point of the line segment joining (2a, 4) and (–2, 2b) is (1, 2a + 1). Find the values of a and b.
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–3, 7), Q(1, –4), a : b = 2 : 1
If the midpoints of the sides ofa triangle are (-2, 3), (4, -3), (4, 5), find its vertices.
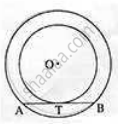
As shown in the figure. two concentric circles are given and line AB is the tangent to the smaller circle at T. Shown that T is the midpoint of Seg AB
If the coordinates of one end of a diameter of a circle is (3, 4) and the coordinates of its centre is (−3, 2), then the coordinate of the other end of the diameter is
In what ratio does the y-axis divides the line joining the points (−5, 1) and (2, 3) internally
Find the coordinates of the mid-point of the line segment with points A(– 2, 4) and B(–6, –6) on both ends.
