SSC (English Medium)
SSC (Marathi Semi-English)
Academic Year: 2021-2022
Date: मार्च 2022
Advertisements
Note:
- All questions are compulsory.
- Use of calculator is not allowed.
- Figures to the right of questions indicates full marks.
- Draw proper figures for answers wherever necessary.
- The marks of construction should be clear and distinct. Do not erase them.
- While writing any proof, drawing relevant figure is necessary. Also the proof should be consistent with the figure.
Four alternative answers for the following question is given. Choose the correct alternative.
Two circles intersect each other such that each circle passes through the centre of the other. If the distance between their centres is 12, what is the radius of each circle?
6 cm
12 cm
24 cm
can’t say
Chapter: [0.03] Circle
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
9 : 25
9 : 16
16 : 9
25 : 9
Chapter: [0.01] Similarity
66 cm
44 cm
160 cm
99 cm
Chapter: [0.07] Mensuration
sin2θ + sin2(90 – θ) = ?
0
1
2
`sqrt(2)`
Chapter: [0.06] Trigonometry
The coordinates of diameter AB of a circle are A(2, 7) and B(4, 5), then find the coordinates of the centre
Chapter: [0.05] Co-ordinate Geometry
`(1 - tan^2 45^circ)/(1 + tan^2 45^circ)` = ?
Chapter: [0.06] Trigonometry
Write the test of similarity for triangles given in figure.
Chapter: [0.01] Similarity
Find distance between point A(7, 5) and B(2, 5)
Chapter: [0.05] Co-ordinate Geometry
Advertisements
The chords corresponding to congruent arcs of a circle are congruent. Prove the theorem by completing following activity.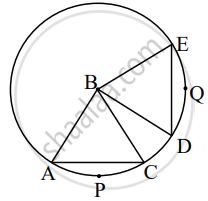
Given: In a circle with centre B
arc APC ≅ arc DQE
To Prove: Chord AC ≅ chord DE
Proof: In ΔABC and ΔDBE,
side AB ≅ side DB ......`square`
side BC ≅ side `square` .....`square`
∠ABC ≅ ∠DBE ......[Measure of congruent arcs]
∆ABC ≅ ∆DBE ......`square`
Chapter: [0.03] Circle
Complete the following activity to find the length of hypotenuse of right angled triangle, if sides of right angle are 9 cm and 12 cm.
Activity: In ∆PQR, m∠PQR = 90°
By Pythagoras Theorem,
PQ2 + `square` = PR2 ......(I)
∴ PR2 = 92 + 122
∴ PR2 = `square` + 144
∴ PR2 = `square`
∴ PR = 15
∴ Length of hypotenuse of triangle PQR is `square` cm.
Chapter: [0.02] Pythagoras Theorem
Find distance between point Q(3, – 7) and point R(3, 3)
Solution: Suppose Q(x1, y1) and point R(x2, y2)
x1 = 3, y1 = – 7 and x2 = 3, y2 = 3
Using distance formula,
d(Q, R) = `sqrt(square)`
∴ d(Q, R) = `sqrt(square - 100)`
∴ d(Q, R) = `sqrt(square)`
∴ d(Q, R) = `square`
Chapter: [0.05] Co-ordinate Geometry
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Chapter: [0.03] Circle
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
Chapter: [0.01] Similarity
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
Chapter: [0.07] Mensuration
A rectangle having dimensions 35 m × 12 m, then what is the length of its diagonal?
Chapter: [0.02] Pythagoras Theorem
If cos(45° + x) = sin 30°, then x = ?
Chapter: [0.06] Trigonometry
Advertisements
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.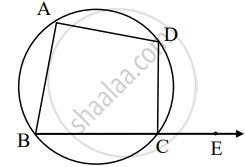
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
Chapter:
From the figure given alongside, find the length of the median AD of triangle ABC. Complete the activity.
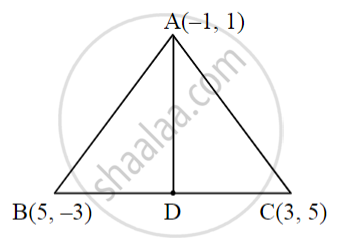
Solution:
Here A(–1, 1), B(5, – 3), C(3, 5) and suppose D(x, y) are coordinates of point D.
Using midpoint formula,
x = `(5 + 3)/2`
∴ x = `square`
y = `(-3 + 5)/2`
∴ y = `square`
Using distance formula,
∴ AD = `sqrt((4 - square)^2 + (1 - 1)^2`
∴ AD = `sqrt((square)^2 + (0)^2`
∴ AD = `sqrt(square)`
∴ The length of median AD = `square`
Chapter: [0.05] Co-ordinate Geometry
In ΔABC, B − D − C and BD = 7, BC = 20, then find the following ratio.
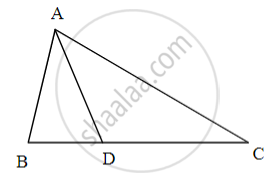
(i) `"A(ΔABD)"/"A(ΔADC)"`
(ii) `"A(ΔABD)"/"A(ΔABC)"`
(iii) `"A(ΔADC)"/"A(ΔABC)"`
Chapter: [0.01] Similarity
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its volume \[\pi\] = 3.14)
Chapter: [0.07] Mensuration
A congruent side of an isosceles right angled triangle is 7 cm, Find its perimeter
Chapter: [0.02] Pythagoras Theorem
Construct an equilateral ∆ABC with side 5 cm. ∆ABC ~ ∆LMN, ratio the corresponding sides of triangle is 6 : 7, then construct ΔLMN and ΔABC
Chapter: [0.04] Geometric Constructions [0.05] Co-ordinate Geometry
In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.
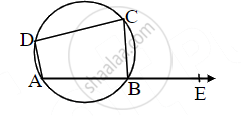
Chapter: [0.03] Circle
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm. Use [π = `22/7`]
Chapter:
ΔAMT ~ ΔAHE. In ΔAMT, AM = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `"AM"/"HA" = 7/5`, then construct ΔAMT and ΔAHE
Chapter: [0.04] Geometric Constructions [0.05] Co-ordinate Geometry
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
Chapter: [0.01] Similarity
In ∆ABC, cos C = `12/13` and BC = 24, then AC = ?
Chapter: [0.06] Trigonometry
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 10th Standard Board Exam Geometry Mathematics 2 with solutions 2021 - 2022
Previous year Question paper for Maharashtra State Board 10th Standard Board Exam Geometry Maths 2-2022 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Geometry Mathematics 2, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 10th Standard Board Exam.
How Maharashtra State Board 10th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Geometry Mathematics 2 will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
