Advertisements
Advertisements
Question
Solution
The radius of the sector of the circle, r = 7 cm
Measure of arc of the sector = θ = 30º
∴ Area of the sector = \[\frac{\theta}{360°} \times \pi r^2 = \frac{30°}{360°} \times \frac{22}{7} \times \left( 7 \right)^2\] = 12.83 cm2
APPEARS IN
RELATED QUESTIONS
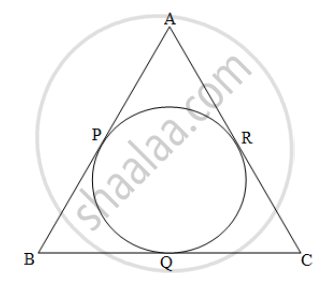
In figure, ΔABC is an isosceles triangle with perimeter 44 cm. The base BC is of length 12 cm. Side AB and side AC are congruent. A circle touches the three sides as shown in the figure below. Find the length of the tangent segment from A to the circle.
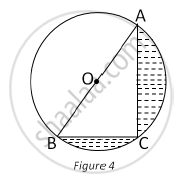
In Fig. 4, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
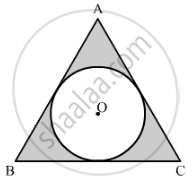
In Fig 4, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.[Use π=3.14 and √3=1.73]
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
The sum of the radii of two circles is 140 cm and the difference of their circumferences in 88 cm. Find the diameters of the circles.
Find in terms of x the length of the arc that subtends an angle of 30°, at the centre of circle of radius 4 cm.
An arc of length 15 cm subtends an angle of 45° at the centre of a circle. Find in terms of 𝜋, radius of the circle.
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that Perimeter of shaded region is 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180`− 1)
The circumference of a circle is 22 cm. Find the area of its quadrant.
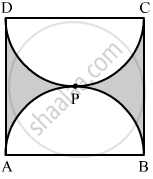
Find the perimeter of the shaded region in the figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles.
A horse is placed for grazing inside a rectangular field 70 m by 52 m. It is tethered to one corner by a rope 21 m long. On how much area can it graze? How much area is left ungrazed?
Four equal circles, each of radius a units, touch each other. Show that the area between them is `(6/7"a"^2)` sq units.
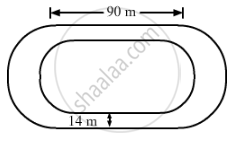
The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.
The sum of diameter of two circles is 112 cm and the sum of their areas is 5236 cm2 Find the radii of the two circles.
The circumference of a circular field is 308 m. Find is:
(i) Radius
(ii) Area.
Complete the table below.
| Radius (r) | Diameter (d) | Circumference (c) |
| ...... | 28 cm | ...... |
The diameter of a circular well is 4.2 m. What is its circumference?
The perimeter of circular and square fields is equal. If the area of the square field is 484 m2 then the diameter of the circular field is ____________.
Circumference of a circle of diameter 5 cm is ______.
