Topics
Integers
- Concept for Natural Numbers
- Concept for Whole Numbers
- Negative and Positive Numbers
- Concept of Integers
- Representation of Integers on the Number Line
- Concept for Ordering of Integers
- Addition of Integers
- Subtraction of Integers
- Properties of Addition and Subtraction of Integers
- Multiplication of a Positive and a Negative Integers
- Multiplication of Two Negative Integers
- Product of Three Or More Negative Integers
- Closure Property of Multiplication of Integers
- Commutative Property of Multiplication of Integers
- Multiplication of Integers with Zero
- Multiplicative Identity of Integers
- Associative Property of Multiplication of Integers
- Distributive Property of Multiplication of Integers
- Making Multiplication Easier of Integers
- Division of Integers
- Properties of Division of Integers
Fractions and Decimals
- Concept of Fractions
- Fraction and its Types
- Concept of Proper Fractions
- Improper Fraction and Mixed Fraction
- Concept of Equivalent Fractions
- Like and Unlike Fraction
- Comparing Fractions
- Addition of Fraction
- Subtraction of Fraction
- Multiplication of a Fraction by a Whole Number
- Fraction as an Operator 'Of'
- Multiplication of Fraction
- Division of Fractions
- Concept of Reciprocal or Multiplicative Inverse
- Problems Based on Fraction
- The Decimal Number System
- Comparing Decimal Numbers
- Addition of Decimal Fraction
- Subtraction of Decimal Numbers
- Multiplication of Decimal Fractions
- Multiplication of Decimal Numbers by 10, 100 and 1000
- Division of Decimal Numbers by 10, 100 and 1000
- Division of Decimal Fractions
- Division of a Decimal Number by Another Decimal Number
- Problems Based on Decimal Numbers
Data Handling
Simple Equations
Lines and Angles
- Concept of Points
- Concept of Line
- Concept of Line Segment
- Concept of Angle
- Complementary Angles
- Supplementary Angles
- Concept of Angle
- Concept of Linear Pair
- Concept of Vertically Opposite Angles
- Concept of Intersecting Lines
- Introduction to Parallel Lines
- Pairs of Lines - Transversal
- Pairs of Lines - Angles Made by a Transversal
- Pairs of Lines - Transversal of Parallel Lines
The Triangle and Its Properties
- Concept of Triangles
- Classification of Triangles (On the Basis of Sides, and of Angles)
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- 3. Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- 3. Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- Median of a Triangle
- Altitudes of a Triangle
- Exterior Angle of a Triangle and Its Property
- Angle Sum Property of a Triangle
- Some Special Types of Triangles - Equilateral and Isosceles Triangles
- Sum of the Lengths of Two Sides of a Triangle
- Right-angled Triangles and Pythagoras Property
Comparing Quantities
- Concept of Ratio
- Concept of Equivalent Ratios
- Concept of Proportion
- Concept of Unitary Method
- Basic Concept of Percentage
- Conversion between Percentage and Fraction
- Converting Decimals to Percentage
- Conversion between Percentage and Fraction
- Converting Percentages to Decimals
- Estimation in Percentages
- Interpreting Percentages
- Converting Percentages to “How Many”
- Ratios to Percents
- Increase Or Decrease as Percent
- Basic Concepts of Profit and Loss
- Profit or Loss as a Percentage
- Calculation of Interest
Congruence of Triangles
Rational Numbers
- Rational Numbers
- Equivalent Rational Number
- Positive and Negative Rational Numbers
- Rational Numbers on a Number Line
- Rational Numbers in Standard Form
- Comparison of Rational Numbers
- Rational Numbers Between Two Rational Numbers
- Addition of Rational Number
- Subtraction of Rational Number
- Multiplication of Rational Numbers
- Division of Rational Numbers
Perimeter and Area
- Mensuration
- Concept of Perimeter
- Perimeter of a Rectangle
- Perimeter of Squares
- Perimeter of Triangles
- Perimeter of Polygon
- Concept of Area
- Area of Square
- Area of Rectangle
- Triangles as Parts of Rectangles and Square
- Generalising for Other Congruent Parts of Rectangles
- Area of a Parallelogram
- Area of a Triangle
- Circumference of a Circle
- Area of Circle
- Conversion of Units
- Problems based on Perimeter and Area
Algebraic Expressions
- Algebraic Expressions
- Terms, Factors and Coefficients of Expression
- Like and Unlike Terms
- Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Evaluation of Algebraic Expressions by Substituting a Value for the Variable.
- Use of Variables in Common Rules
Practical Geometry
- Construction of a Line Parallel to a Given Line, Through a Point Not on the Line
- Construction of Triangles
- Constructing a Triangle When the Length of Its Three Sides Are Known (SSS Criterion)
- Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle Between Them Are Known. (SAS Criterion)
- Constructing a Triangle When the Measures of Two of Its Angles and the Length of the Side Included Between Them is Given. (ASA Criterion)
- Constructing a Right-angled Triangle When the Length of One Leg and Its Hypotenuse Are Given (RHS Criterion)
Exponents and Powers
- Concept of Exponents
- Multiplying Powers with the Same Base
- Dividing Powers with the Same Base
- Taking Power of a Power
- Multiplying Powers with Different Base and Same Exponents
- Dividing Powers with Different Base and Same Exponents
- Numbers with Exponent Zero, One, Negative Exponents
- Miscellaneous Examples Using the Laws of Exponents
- Decimal Number System Using Exponents and Powers
- Crores
Symmetry
Visualizing Solid Shapes
- Introduction
- Methods of Comparing Fraction
Introduction
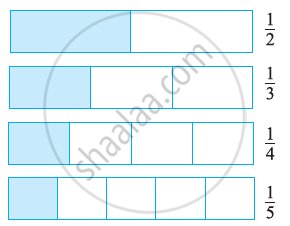
Consider `1/2 and 1/3`
The portion of the whole corresponding to `1/2` is clearly larger than the portion of the same whole corresponding to `1/3`. But often it is difficult to say which one out of a pair of fractions is larger. We should, therefore, like to have a systematic procedure to compare fractions. It is particularly easy to compare like fractions.
Methods of Comparing Fraction
1. Comparing like fractions
Let us compare two like rational numbers: `3/8 and 5/8`.
In both fractions, the whole is divided into 8 equal parts. For `3/8 and 5/8`, When comparing fractions with the same denominator, the fraction with the greater numerator is larger.
Hence, `5/8 > 3/8`.
eg.`4/5 and 3/5, 4/5` is greater.
2. Comparing unlike fractions
Compare `5/6 and 13/15`.
Solution: The fractions are unlike. We should first get their equivalent fractions with a denominator that is a common multiple of 6 and 15.
Now, `(5 × 5)/(6 × 5) = 25/30, (13 × 2)/(15 × 2) = (26)/(30)`
Since, `(26/30) > (25/30) "we have" (13/15) > (5/6)`
3. Comparing unlike fractions with the same numerators: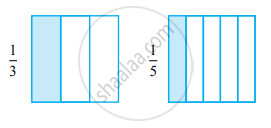
In `1/3`, we divide the whole into 3 equal parts and take one. In `1/5`, we divide the whole into 5 equal parts and take one.
When two fractions have the same numerator, the fraction with the smaller denominator is greater. This is because dividing a whole into fewer parts results in larger individual parts.
Hence, `1/3 > 1/5`.
Example
Find answers to the following. Write and indicate how you solved them.
Is `5/9` equal to `4/5`?
`5/9, 4/5`
Converting these into like fractions,
`5/9 = 5/9 xx 5/5 = 25/45`
`4/5 = 4/5 xx 9/9 = 36/45`
As, `36/45 ≠ 25/45`,
Therefore, `5/9 "is not equal to" 4/5`.
Example
Find answers to the following. Write and indicate how you solved them.
Is `9/16` equal to `5/9`?
`9/16, 5/9`
Converting these into like fractions,
`9/16 = 9/16 xx 9/9 = 81/144`
`5/9 = 5/9 xx 16/16 = 80/144`
As, `81/144 ≠ 80/144`,
Therefore, `9/16 "is not equal to" 5/9`.
Example
Find answers to the following. Write and indicate how you solved them.
Is `4/5` equal to `16/20`?
`4/5, 16/20`
`16/20 = (4 xx 4)/(5 xx 4) = 4/5`
Therefore, `4/5 = 16/20`.
Example
Ila read 25 pages of a book containing 100 pages. Lalita read `2/5` of the same book. Who reads less?
Numbers of pages read by Lalita = `2/5 xx 100` = 40
Number of pages read by Ila = 25
Hence, Ila has read less number of pages.
Example
Asha and Samuel have bookshelves of the same size partly filled with books. Asha’s shelf is `5/6`th full and Samuel’s shelf is `2/5`th full. Whose bookshelf is more full? By what fraction?
Fraction of Asha’s shelf = `5/6`
Fraction of Samuel’s shelf = `2/5`
Converting these into like fractions,
`5/6 = 5/6 xx 5/5 = 25/30`
`2/5 = 2/5 xx 6/6 = 12/30`
`25/30 > 12/30`
Clearly, Asha’s bookshelf is more full.
Difference = `5/6 - 2/5 = 25/30 - 12/30 = 13/30`.
Example
Jaidev takes `2 1/5` minutes to walk across the school ground. Rahul takes `7/4` minutes to do the same. Who takes less time and by what fraction?
Time taken by Jaidev = `2 1/5 "minutes" = 11/5` min
Time taken by Rahul = `7/4` min
Converting these into like fractions,
`11/5 = 11/5 xx 4/4 = 44/20`
`7/4 = 7/4 xx 5/5 = 35/20`
As 44 > 35,
`11/5 > 7/4`
Hence, Rahul takes lesser time.
Difference = `11/5 - 7/4`
= `44/20 - 35/20 = 9/20` min.
Shaalaa.com | Comparison Of Like Fractions
Series: Comparing Fractions
00:09:30 undefined
00:11:20 undefined
00:10:59 undefined
00:10:56 undefined
00:09:42 undefined
00:07:40 undefined
00:07:25 undefined