3. Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled

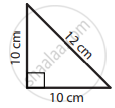
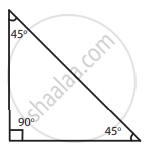
Right-angled Triangle: A right triangle is a triangle in which one angle has a measurement of 90°.

Acute Angled Triangle: An acute triangle is defined as a triangle in which all of the angles are less than 90°.

Obtuse angled Triangle: An obtuse triangle is one that has an angle greater than 90°.

Right Angled Triangle:

• A right triangle is a triangle in which one angle has a measurement of 90°.
• Right angles are typically denoted by a square drawn at the vertex of the angle that is a right angle.
• The side opposite the right angle of a right triangle is called the hypotenuse. The hypotenuse is the longest side of the right triangle.
• The sides that form the right angle are called legs. 

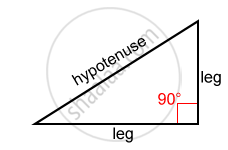
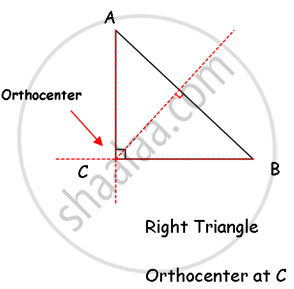
Properties Of Right-angled Triangle:

• A right triangle has a 90 degrees angle. This triangle consists of one right angle and two acute angles.
• The right angle is an angle that measures 90° and the acute angles are those angles that measure less than 90°.
• The orthocenter is the point where all three altitudes of the triangle intersect. The orthocenter of the right-angled triangle is located at c.

Acute Angled Triangle:

• An acute triangle is defined as a triangle in which all of the angles are less than 90°. In other words, all of the angles in an acute triangle are acute.

Properties of Acute Triangles:

• All equilateral triangles are acute triangles. An equilateral triangle has three sides of equal length and three equal angles of 60°.
• Acute triangles can be isosceles, equilateral, or scalene.
• The longest side of an acute triangle is opposite the largest angle. The greater the measure of an angle opposite side, the longer the side. Conversely, the longer the side the greater the measure of the opposing angle.
• The orthocenter is the point where all three altitudes of the triangle intersect. The orthocenter for an acute triangle is located inside of the triangle.
  

Obtuse angled Triangle:

• An obtuse triangle is one that has an angle greater than 90°. Because all the angles in a triangle add up to 180°, the other two angles have to be acute (less than 90°). It's impossible for a triangle to have more than one obtuse angle.

Properties of obtuse triangles:

• Whenever a triangle is classified as obtuse, one of its interior angles has a measure between 90 and 180 degrees.
• An obtuse triangle has only one angle greater than 90° since the sum of the angles in any triangle is 180°. If one of the angles is greater than 90°, then the sum of the other two angles must be less than 90°, so the other two angles must both be acute angles.

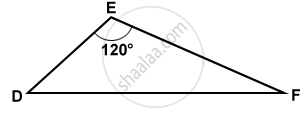
      For △DEF above, ∠D + ∠F = 60° < 90°, so ∠D and ∠F are acute angles.

• The side opposite the obtuse angle for an obtuse triangle is the longest side of the triangle. The greater the angle, the longer the side opposite it. Conversely, the longer the side, the greater the angle opposite it.
• An obtuse triangle may be either isosceles (two equal sides and two equal angles) or scalene (no equal sides or angles).
• The orthocenter is the point where all three altitudes of the triangle intersect. The orthocenter of an obtuse triangle is located outside of the triangle.