Topics
Rational Numbers
- Rational Numbers
- Closure Property of Rational Numbers
- Commutative Property of Rational Numbers
- Associative Property of Rational Numbers
- Distributive Property of Multiplication Over Addition for Rational Numbers
- Identity of Addition and Multiplication of Rational Numbers
- Negative Or Additive Inverse of Rational Numbers
- Concept of Reciprocal or Multiplicative Inverse
- Rational Numbers on a Number Line
- Rational Numbers Between Two Rational Numbers
Linear Equations in One Variable
- Variable of Equation
- Concept of Equation
- Expressions with Variables
- Balancing an Equation
- The Solution of an Equation
- Linear Equation in One Variable
- Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side
- Some Applications Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side
- Solving Equations Having the Variable on Both Sides
- Some More Applications on the Basis of Solving Equations Having the Variable on Both Sides
- Reducing Equations to Simpler Form
- Equations Reducible to the Linear Form
Understanding Quadrilaterals
- Concept of Curves
- Different Types of Curves - Closed Curve, Open Curve, Simple Curve.
- Concept of Polygons
- Classification of Polygons
- Properties of a Quadrilateral
- Interior Angles of a Polygon
- Exterior Angles of a Polygon and Its Property
- Concept of Quadrilaterals
- Properties of Trapezium
- Properties of Kite
- Properties of a Parallelogram
- Properties of Rhombus
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Property: The adjacent angles in a parallelogram are supplementary.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Property: The diagonals of a rhombus are perpendicular bisectors of one another.
- Property: The Diagonals of a Rectangle Are of Equal Length.
- Properties of Rectangle
- Properties of a Square
- Property: The diagonals of a square are perpendicular bisectors of each other.
Practical Geometry
- Introduction to Geometric Tool
- Constructing a Quadrilateral When the Lengths of Four Sides and a Diagonal Are Given
- Constructing a Quadrilateral When Two Diagonals and Three Sides Are Given
- Constructing a Quadrilateral When Two Adjacent Sides and Three Angles Are Known
- Constructing a Quadrilateral When Three Sides and Two Included Angles Are Given
- Some Special Cases
Data Handling
- Concept of Data Handling
- Interpretation of a Pictograph
- Interpretation of Bar Graphs
- Drawing a Bar Graph
- Interpretation of a Double Bar Graph
- Drawing a Double Bar Graph
- Organisation of Data
- Frequency Distribution Table
- Graphical Representation of Data as Histograms
- Concept of Pie Graph (Or a Circle-graph)
- Interpretation of Pie Diagram
- Chance and Probability - Chance
- Basic Ideas of Probability
Squares and Square Roots
- Concept of Square Number
- Properties of Square Numbers
- Some More Interesting Patterns of Square Number
- Finding the Square of a Number
- Concept of Square Roots
- Finding Square Root Through Repeated Subtraction
- Finding Square Root Through Prime Factorisation
- Finding Square Root by Division Method
- Square Root of Decimal Numbers
- Estimating Square Root
Cubes and Cube Roots
Comparing Quantities
- Concept of Ratio
- Basic Concept of Percentage
- Increase Or Decrease as Percent
- Concept of Discount
- Estimation in Percentages
- Basic Concepts of Profit and Loss
- Sales Tax, Value Added Tax, and Good and Services Tax
- Calculation of Interest
- Concept of Compound Interest
- Deducing a Formula for Compound Interest
- Rate Compounded Annually Or Half Yearly (Semi Annually)
- Applications of Compound Interest Formula
Algebraic Expressions and Identities
- Algebraic Expressions
- Terms, Factors and Coefficients of Expression
- Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials
- Like and Unlike Terms
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Multiplication of Algebraic Expressions
- Multiplying Monomial by Monomials
- Multiplying a Monomial by a Binomial
- Multiplying a Monomial by a Trinomial
- Multiplying a Binomial by a Binomial
- Multiplying a Binomial by a Trinomial
- Concept of Identity
- Expansion of (a + b)2 = a2 + 2ab + b2
- Expansion of (a - b)2 = a2 - 2ab + b2
- Expansion of (a + b)(a - b) = a2-b2
- Expansion of (x + a)(x + b)
Mensuration
Visualizing Solid Shapes
Exponents and Powers
Direct and Inverse Proportions
Factorization
- Factors and Multiples
- Factorising Algebraic Expressions
- Factorisation by Taking Out Common Factors
- Factorisation by Regrouping Terms
- Factorisation Using Identities
- Factors of the Form (x + a)(x + b)
- Dividing a Monomial by a Monomial
- Dividing a Polynomial by a Monomial
- Dividing a Polynomial by a Polynomial
- Concept of Find the Error
Introduction to Graphs
- Concept of Bar Graph
- Interpretation of Bar Graphs
- Drawing a Bar Graph
- Concept of Double Bar Graph
- Interpretation of a Double Bar Graph
- Drawing a Double Bar Graph
- Concept of Pie Graph (Or a Circle-graph)
- Graphical Representation of Data as Histograms
- Concept of a Line Graph
- Linear Graphs
- Some Application of Linear Graphs
Playing with Numbers
Notes
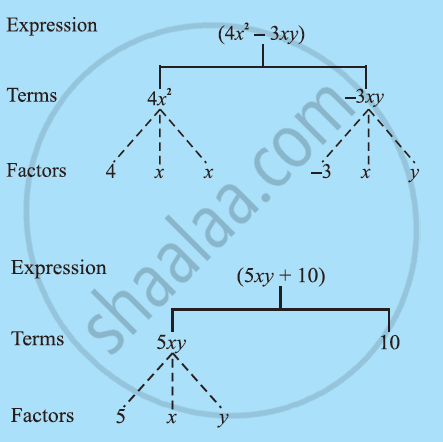
Terms, Factors and Coefficients of Expression:
1. Terms:
-
Terms are added to form expressions. Terms are added to make an expression.
-
For example, the terms 4x2 and (- 3xy) are added to give the expression 4x2 – 3xy. This is because 4x2 + (- 3xy) = 4x2 – 3xy.
-
Note, the minus sign (–) is included in the term.
2. Factors:
A term is a product of factors. The term 4xy in the expression 4xy + 7 is a product of factors x, y, and 4. Factors containing variables are said to be algebraic factors.
The expression (4x2 – 3xy) consists of two terms 4x2 and – 3xy. The term 4x2 is a product of 4, x, and x; we say that 4, x, and x are the factors of the term 4x2. A term is a product of its factors. The term – 3xy is a product of the factors –3, x, and y.
3. Coefficient:
-
The coefficient is the numerical factor in the term. Sometimes any one factor in a term is called the coefficient of the remaining part of the term.
-
In the term 10xyz, 10 is the coefficient of xyz, in the term -7x2y2, - 7 is the coefficient of x2y2.
- When the coefficient of a term is + 1, it is usually omitted. For example, 1x is written as x; 1x2y2 is written as x2y2, and so on. Also, the coefficient (– 1) is indicated only by the minus sign.
Thus (– 1) x is written as – x; (–1) x2 y 2 is written as – x2 y2 and so on.
- Sometimes, the word 'coefficient' is used in a more general way. Thus we say that in the term 5xy, 5 is the coefficient of xy, x is the coefficient of 5y and y is the coefficient of 5x. In 10xy2, 10 is the coefficient of xy2, x is the coefficient of 10y2 and y2 is the coefficient of 10x.
Thus, in this more general way, a coefficient may be either a numerical factor or an algebraic factor or a product of two or more factors. It is said to be the coefficient of the product of the remaining factors.
-
The coefficient is the numerical factor in the term. Sometimes any one factor in a term is called the coefficient of the remaining part of the term.
-
In the term 10xyz, 10 is the coefficient of xyz, in the term -7x2y2, - 7 is the coefficient of x2y2.
- When the coefficient of a term is + 1, it is usually omitted. For example, 1x is written as x; 1x2y2 is written as x2y2, and so on. Also, the coefficient (– 1) is indicated only by the minus sign.
Thus (– 1) x is written as – x; (–1) x2 y 2 is written as – x2 y2 and so on. - Sometimes, the word 'coefficient' is used in a more general way. Thus we say that in the term 5xy, 5 is the coefficient of xy, x is the coefficient of 5y and y is the coefficient of 5x. In 10xy2, 10 is the coefficient of xy2, x is the coefficient of 10y2 and y2 is the coefficient of 10x.
Thus, in this more general way, a coefficient may be either a numerical factor or an algebraic factor or a product of two or more factors. It is said to be the coefficient of the product of the remaining factors.
Shaalaa.com | Terms of Algebraic Expression
Related QuestionsVIEW ALL [271]
Observe the following nutritional chart carefully:
| Food Item (Per Unit = 100g) | Carbohydrates |
| Rajma | 60g |
| Cabbage | 5g |
| Potato | 22g |
| Carrot | 11g |
| Tomato | 4g |
| Apples | 14g |
Write an algebraic expression for the amount of carbohydrates (in grams) for 2x units tomatoes and y units apples.
