Topics
Rational Numbers
- Rational Numbers
- Closure Property of Rational Numbers
- Commutative Property of Rational Numbers
- Associative Property of Rational Numbers
- Distributive Property of Multiplication Over Addition for Rational Numbers
- Identity of Addition and Multiplication of Rational Numbers
- Negative Or Additive Inverse of Rational Numbers
- Concept of Reciprocal or Multiplicative Inverse
- Rational Numbers on a Number Line
- Rational Numbers Between Two Rational Numbers
Linear Equations in One Variable
- Variable of Equation
- Concept of Equation
- Expressions with Variables
- Balancing an Equation
- The Solution of an Equation
- Linear Equation in One Variable
- Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side
- Some Applications Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side
- Solving Equations Having the Variable on Both Sides
- Some More Applications on the Basis of Solving Equations Having the Variable on Both Sides
- Reducing Equations to Simpler Form
- Equations Reducible to the Linear Form
Understanding Quadrilaterals
- Concept of Curves
- Different Types of Curves - Closed Curve, Open Curve, Simple Curve.
- Concept of Polygons
- Classification of Polygons
- Properties of a Quadrilateral
- Interior Angles of a Polygon
- Exterior Angles of a Polygon and Its Property
- Concept of Quadrilaterals
- Properties of Trapezium
- Properties of Kite
- Properties of a Parallelogram
- Properties of Rhombus
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Property: The adjacent angles in a parallelogram are supplementary.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Property: The diagonals of a rhombus are perpendicular bisectors of one another.
- Property: The Diagonals of a Rectangle Are of Equal Length.
- Properties of Rectangle
- Properties of a Square
- Property: The diagonals of a square are perpendicular bisectors of each other.
Practical Geometry
- Introduction to Geometric Tool
- Constructing a Quadrilateral When the Lengths of Four Sides and a Diagonal Are Given
- Constructing a Quadrilateral When Two Diagonals and Three Sides Are Given
- Constructing a Quadrilateral When Two Adjacent Sides and Three Angles Are Known
- Constructing a Quadrilateral When Three Sides and Two Included Angles Are Given
- Some Special Cases
Data Handling
- Concept of Data Handling
- Interpretation of a Pictograph
- Interpretation of Bar Graphs
- Drawing a Bar Graph
- Interpretation of a Double Bar Graph
- Drawing a Double Bar Graph
- Organisation of Data
- Frequency Distribution Table
- Graphical Representation of Data as Histograms
- Concept of Pie Graph (Or a Circle-graph)
- Interpretation of Pie Diagram
- Chance and Probability - Chance
- Basic Ideas of Probability
Squares and Square Roots
- Concept of Square Number
- Properties of Square Numbers
- Some More Interesting Patterns of Square Number
- Finding the Square of a Number
- Concept of Square Roots
- Finding Square Root Through Repeated Subtraction
- Finding Square Root Through Prime Factorisation
- Finding Square Root by Division Method
- Square Root of Decimal Numbers
- Estimating Square Root
Cubes and Cube Roots
Comparing Quantities
- Concept of Ratio
- Basic Concept of Percentage
- Increase Or Decrease as Percent
- Concept of Discount
- Estimation in Percentages
- Basic Concepts of Profit and Loss
- Sales Tax, Value Added Tax, and Good and Services Tax
- Calculation of Interest
- Concept of Compound Interest
- Deducing a Formula for Compound Interest
- Rate Compounded Annually Or Half Yearly (Semi Annually)
- Applications of Compound Interest Formula
Algebraic Expressions and Identities
- Algebraic Expressions
- Terms, Factors and Coefficients of Expression
- Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials
- Like and Unlike Terms
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Multiplication of Algebraic Expressions
- Multiplying Monomial by Monomials
- Multiplying a Monomial by a Binomial
- Multiplying a Monomial by a Trinomial
- Multiplying a Binomial by a Binomial
- Multiplying a Binomial by a Trinomial
- Concept of Identity
- Expansion of (a + b)2 = a2 + 2ab + b2
- Expansion of (a - b)2 = a2 - 2ab + b2
- Expansion of (a + b)(a - b) = a2-b2
- Expansion of (x + a)(x + b)
Mensuration
Visualizing Solid Shapes
Exponents and Powers
Direct and Inverse Proportions
Factorization
- Factors and Multiples
- Factorising Algebraic Expressions
- Factorisation by Taking Out Common Factors
- Factorisation by Regrouping Terms
- Factorisation Using Identities
- Factors of the Form (x + a)(x + b)
- Dividing a Monomial by a Monomial
- Dividing a Polynomial by a Monomial
- Dividing a Polynomial by a Polynomial
- Concept of Find the Error
Introduction to Graphs
- Concept of Bar Graph
- Interpretation of Bar Graphs
- Drawing a Bar Graph
- Concept of Double Bar Graph
- Interpretation of a Double Bar Graph
- Drawing a Double Bar Graph
- Concept of Pie Graph (Or a Circle-graph)
- Graphical Representation of Data as Histograms
- Concept of a Line Graph
- Linear Graphs
- Some Application of Linear Graphs
Playing with Numbers
Notes
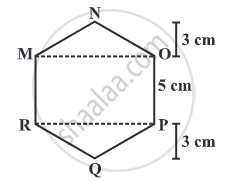
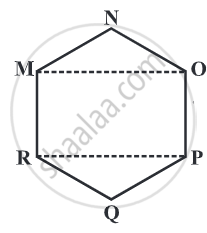
Area of a Polygon:
We split a quadrilateral into triangles and find its area. Similar methods can be used to find the area of a polygon.
Polygon refers to a closed 2D shape which is made up of a finite number of line segments.
Steps to find the area of a polygon:
-
Divide the polygons into parts (triangles, trapezium, rectangle, square, and parallelogram) to find out its area.
-
Adding the area of all triangles and trapeziums.
Some of the ways to find the area are shown below:
Divide the polygons into parts (triangles, trapezium, rectangle, square, and parallelogram) to find out its area.
Adding the area of all triangles and trapeziums.
1)
By constructing two diagonals AC and AD the pentagon ABCDE is divided into three parts.
So, Area ABCDE = Area of ∆ABC + Area of ∆ACD + Area of ∆AED.
2)
By constructing one diagonal AD and two perpendiculars BF and CG on it, pentagon ABCDE is divided into four parts.
So, Area of ABCDE = Area of right-angled ∆AFB + Area of trapezium BFGC + Area of right-angled ∆CGD + Area of ∆AED.
3)
Area of hexagon MNOPQR = Area of Triangle MNO + Area of Triangle RPQ + Area of Rectangle MOPR.
4)
Area of this polygon = area of 2 trapeziums.
Example
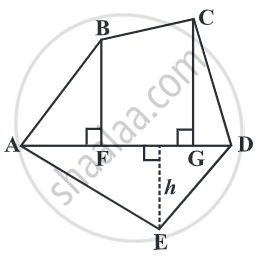
Polygon ABCDE is divided in different parts as shown in figure. If AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and BF = 2 cm, CH = 3cm, EG = 2.5 cm. Then find the area of the polygon.
Area of polygon ABCDE = Area of right ΔAFB + Area of trapezium BFHC + Area of right ΔCHD + Area of right ΔEGD + Area of right ΔAGE
`= 1/2 xx "AF" xx "BF" + 1/2 xx ["BF + CH"] xx "FH" + 1/2 xx "HD" xx "CH" + 1/2 xx "GD" xx "GE" + 1/2 xx "AG" xx "GE"`
`= 1/2 xx 3 xx 2 + 1/2 xx [2 + 3] xx [6 – 3] + 1/2 xx [8 – 6] xx 3 + 1/2 xx [8 – 4] xx 2.5 + 1/2 xx 4 xx 2.5`
= 3 + 7.5 + 3 + 5 + 5
= 23.5 cm2
Example
The area of a trapezium-shaped field is 480 m2, the distance between two parallel sides is 15 m and one of the parallel sides is 20 m. Find the other parallel side.
One of the parallel sides of the trapezium is a = 20 m, let another parallel side be b, height h = 15 m.
The given area of trapezium = 480 m2.
Area of a trapezium = `1/2` h(a + b)
So, 480 = `1/2` × 15 × (20 + b)
or `(480 xx 2)/15 = 20 + b`
or `(480 xx 2)/15 = 20 + b`
or 64 = 20 + b
or b = 44 m.
Hence the other parallel side of the trapezium is 44 m.
Example
There is a hexagon MNOPQR of side 5 cm. Aman and Ridhima divided it into two different ways. Find the area of this hexagon using both ways.
Aman’s method:
Since it is a hexagon so NQ divides the hexagon into two congruent trapeziums.
Now area of trapezium MNQR = `4 xx ((11 + 5))/2 = 2 xx 16 = 32` cm2
So the area of hexagon MNOPQR = 2 × 32 = 64 cm2.
Ridhima’s method:
∆MNO and ∆RPQ are congruent triangles with an altitude of 3 cm.
Area of ∆MNO = `1/2 xx 8 xx 3` = 12 cm2 = Area of ∆ RPQ
Area of rectangle MOPR = 8 × 5 = 40 cm2.
Now, area of hexagon MNOPQR = 40 + 12 + 12 = 64 cm2.
If you would like to contribute notes or other learning material, please submit them using the button below.
Shaalaa.com | Problems on Finding Area of a Polygon - Part 1
to track your progress
