Advertisements
Advertisements
Question
Find the area of the following regular hexagon.
Solution
Join QN.

It is given that the hexagon is regular. So, all its sides must be equal to 13 cm.
Also, AN = BQ
QB+BA+AN = QN
AN+13+AN = 23
2AN = 23-13 = 10
\[AN =\frac{10}{2}= 5 cm\]
Hence, AN = BQ = 5 cm
Now, in the right angle triangle MAN:
\[ {MN}^2 {=AN}^2 {+AM}^2 \]
\[ {13}^2 {=5}^2 {+AM}^2 \]
\[ {AM}^2 =169-25=144\]
\[AM=\sqrt{144}=12cm.\]
\[\therefore OM = RP = 2\times AM = 2\times12 = 24 cm\]
Hence, area of the regular hexagon = (area of triangle MON)+(area of rectangle MOPR)+(area of triangle RPQ)
\[=(\frac{1}{2}\times OM\times AN)+(RP\times PO)+(\frac{1}{2}\times RP\times BQ)\]
\[=(\frac{1}{2}\times24\times5)+(24\times13)+(\frac{1}{2}\times24\times5)\]
\[=60+312+60\]
\[ {=432 cm}^2\]
APPEARS IN
RELATED QUESTIONS
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
The area of a rhombus is 240 cm2 and one of the diagonal is 16 cm. Find another diagonal.
Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
The length of a side of a square field is 4 m. what will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonal is 2 m?
The cost of fencing a square field at 60 paise per metre is Rs 1200. Find the cost of reaping the field at the rate of 50 paise per 100 sq. metres.
The area of a rhombus is equal to the area of a triangle whose base and the corresponding altitude are 24.8 cm and 16.5 cm respectively. If one of the diagonals of the rhombus is 22 cm, find the length of the other diagonal.
Find the area of the following polygon, if AL = 10 cm, AM = 20 cm, AN = 50 cm, AO = 60 cm and AD = 90 cm.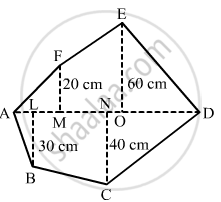
Polygon ABCDE is divided in different parts as shown in figure. If AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and BF = 2 cm, CH = 3cm, EG = 2.5 cm. Then find the area of the polygon.

A regular hexagon is inscribed in a circle of radius r. The perimeter of the regular hexagon is ______.
