Advertisements
Advertisements
Question
The length of a side of a square field is 4 m. what will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonal is 2 m?
Solution
Length of the square field = 4 m
∴ A {rea of the square field = 4 x 4 = 16 m}2
Given: Area of the rhombus = Area of the square field
Length of one diagonal of the rhombus = 2 m
∴ Side of the rhombus \[=\frac{1}{2}\sqrt{d_1^2 + d_2^2}\]
And, area of the rhombus \[=\frac{1}{2} \times ( d_1 \times d_2 )\]
∴ Area:
\[16 = \frac{1}{2}(2 \times d_2 )\]
\[ d_2 =16 m\]
Now, we need to find the length of the side of the rhombus.
∴ Side of the rhombus \[=\frac{1}{2}\sqrt{2^2 + {16}^2}=\frac{1}{2}\sqrt{260}=\frac{1}{2}\sqrt{4 \times 65}=\frac{1}{2}\times2\sqrt{65}=\sqrt{65}m\]
Also, we know: Area of the rhombus = Side X Altitude
\[ \therefore 16=\sqrt{65}\times \] Altitude
Altitude \[=\frac{16}{\sqrt{65}}m\]
APPEARS IN
RELATED QUESTIONS
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.

Find the area of this park using both ways. Can you suggest some other way of finding its area?
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Find the area of the field in the form of a rhombus, if the length of each side be 14 cm and the altitude be 16 cm.
The area of a rhombus is 84 m2. If its perimeter is 40 m, then find its altitude.
Find the area of the following polygon, if AL = 10 cm, AM = 20 cm, AN = 50 cm, AO = 60 cm and AD = 90 cm.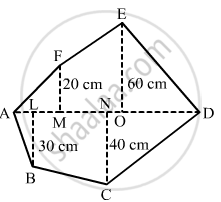
Find the area of the following regular hexagon.
Polygon ABCDE is divided in different parts as shown in figure. If AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and BF = 2 cm, CH = 3cm, EG = 2.5 cm. Then find the area of the polygon.

A regular hexagon is inscribed in a circle of radius r. The perimeter of the regular hexagon is ______.
