Advertisements
Advertisements
Question
Find the area of the following polygon, if AL = 10 cm, AM = 20 cm, AN = 50 cm, AO = 60 cm and AD = 90 cm.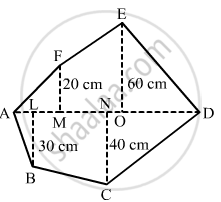
Advertisements
Solution
The given polygon is:
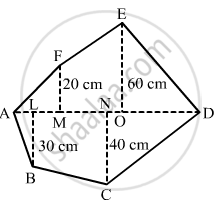
Given:
AL=10 cm, AM=20 cm, AN=50 cm
\[AO=60 cm, AD=90 cm\]
Hence, we have the following:
\[MO=AO-AM=60-20=40 cm\]
\[OD=AD-AO=90-60=30 cm\]
\[ND=AD-AN=90-50=40 cm\]
\[LN=AN-AL=50-10=40 cm\]
From given figure:
Area of Polygon=(Area of triangle AMF)+(Area of trapezium MOEF)+(Area of triangle EOD)+(Area of triangle DNC)+ (Area of trapezium NLBC )+(Area of triangle ALB)
\[=(\frac{1}{2}\times AM\times MF)+[\frac{1}{2} \times (MF+OE)\times(OM)]+(\frac{1}{2}\times OD\times OE)+(\frac{1}{2}\times DN\times NC) +[ \frac{1}{2} \times (LB+NC)\times(NL)]+(\frac{1}{2} \times AL\times LB)\]
\[=(\frac{1}{2}\times20\times20)+[\frac{1}{2} \times (20+60)\times(40)]+(\frac{1}{2} \times 30\times60)+(\frac{1}{2}\times40\times40) +[ \frac{1}{2} \times (30+40)\times(40)]+(\frac{1}{2} \times 10 \times 30)\]
\[=200+1600+900+800+1400+150\]
\[ {=5050 cm}^2\]
RELATED QUESTIONS
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
The floor of a building consists of 3000 tiles, which are rhombus shaped, and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor if the cost per m2 is ₹ 4.
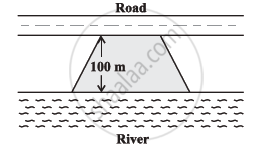
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. It the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2?
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs 4.
A rectangular grassy plot is 112 m long and 78 m broad. It has a gravel path 2.5 m wide all around it on the side. Find the area of the path and the cost of constructing it at Rs 4.50 per square metre.
The cost of fencing a square field at 60 paise per metre is Rs 1200. Find the cost of reaping the field at the rate of 50 paise per 100 sq. metres.
In exchange of a square plot one of whose sides is 84 m, a man wants to buy a rectangular plot 144 m long and of the same area as of the square plot. Find the width of the rectangular plot.
The area of a rhombus is 84 m2. If its perimeter is 40 m, then find its altitude.
