Advertisements
Advertisements
प्रश्न
Find the area of the following polygon, if AL = 10 cm, AM = 20 cm, AN = 50 cm, AO = 60 cm and AD = 90 cm.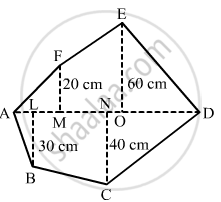
उत्तर
The given polygon is:
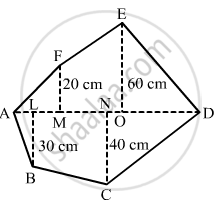
Given:
AL=10 cm, AM=20 cm, AN=50 cm
\[AO=60 cm, AD=90 cm\]
Hence, we have the following:
\[MO=AO-AM=60-20=40 cm\]
\[OD=AD-AO=90-60=30 cm\]
\[ND=AD-AN=90-50=40 cm\]
\[LN=AN-AL=50-10=40 cm\]
From given figure:
Area of Polygon=(Area of triangle AMF)+(Area of trapezium MOEF)+(Area of triangle EOD)+(Area of triangle DNC)+ (Area of trapezium NLBC )+(Area of triangle ALB)
\[=(\frac{1}{2}\times AM\times MF)+[\frac{1}{2} \times (MF+OE)\times(OM)]+(\frac{1}{2}\times OD\times OE)+(\frac{1}{2}\times DN\times NC) +[ \frac{1}{2} \times (LB+NC)\times(NL)]+(\frac{1}{2} \times AL\times LB)\]
\[=(\frac{1}{2}\times20\times20)+[\frac{1}{2} \times (20+60)\times(40)]+(\frac{1}{2} \times 30\times60)+(\frac{1}{2}\times40\times40) +[ \frac{1}{2} \times (30+40)\times(40)]+(\frac{1}{2} \times 10 \times 30)\]
\[=200+1600+900+800+1400+150\]
\[ {=5050 cm}^2\]
APPEARS IN
संबंधित प्रश्न
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2?
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
The length of a side of a square field is 4 m. what will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonal is 2 m?
In exchange of a square plot one of whose sides is 84 m, a man wants to buy a rectangular plot 144 m long and of the same area as of the square plot. Find the width of the rectangular plot.
The area of a rhombus is 84 m2. If its perimeter is 40 m, then find its altitude.
A field in the form of a rhombus has each side of length 64 m and altitude 16 m. What is the side of a square field which has the same area as that of a rhombus?
The area of a rhombus is equal to the area of a triangle whose base and the corresponding altitude are 24.8 cm and 16.5 cm respectively. If one of the diagonals of the rhombus is 22 cm, find the length of the other diagonal.
A regular hexagon is inscribed in a circle of radius r. The perimeter of the regular hexagon is ______.
