Advertisements
Advertisements
प्रश्न
Find the area of the following regular hexagon.
उत्तर
Join QN.

It is given that the hexagon is regular. So, all its sides must be equal to 13 cm.
Also, AN = BQ
QB+BA+AN = QN
AN+13+AN = 23
2AN = 23-13 = 10
\[AN =\frac{10}{2}= 5 cm\]
Hence, AN = BQ = 5 cm
Now, in the right angle triangle MAN:
\[ {MN}^2 {=AN}^2 {+AM}^2 \]
\[ {13}^2 {=5}^2 {+AM}^2 \]
\[ {AM}^2 =169-25=144\]
\[AM=\sqrt{144}=12cm.\]
\[\therefore OM = RP = 2\times AM = 2\times12 = 24 cm\]
Hence, area of the regular hexagon = (area of triangle MON)+(area of rectangle MOPR)+(area of triangle RPQ)
\[=(\frac{1}{2}\times OM\times AN)+(RP\times PO)+(\frac{1}{2}\times RP\times BQ)\]
\[=(\frac{1}{2}\times24\times5)+(24\times13)+(\frac{1}{2}\times24\times5)\]
\[=60+312+60\]
\[ {=432 cm}^2\]
APPEARS IN
संबंधित प्रश्न
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
The floor of a building consists of 3000 tiles, which are rhombus shaped, and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor if the cost per m2 is ₹ 4.
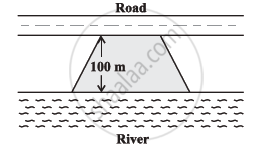
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. It the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.

Find the area of this park using both ways. Can you suggest some other way of finding its area?
The area of a rhombus is 240 cm2 and one of the diagonal is 16 cm. Find another diagonal.
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
The length of a side of a square field is 4 m. what will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonal is 2 m?
A field in the form of a rhombus has each side of length 64 m and altitude 16 m. What is the side of a square field which has the same area as that of a rhombus?

