Advertisements
Advertisements
प्रश्न
Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
Advertisements
उत्तर
Given:
Side of the rhombus = 20 cm
Length of a diagonal = 24 cm
We know: If `d_1` and `d_2` are the lengths of the diagonals of the rhombus, then
side of the rhombus\[= \frac{1}{2}\sqrt{d_1^2 + d_2^2}\]
So, using the given data to find the length of the other diagonal of the rhombus:
\[20 = \frac{1}{2}\sqrt{{24}^2 + d_2^2}\]
\[40 = \sqrt{{24}^2 + d_2^2}\]
Squaring both sides to get rid of the square root sign:
\[ {40}^2 = {24}^2 + d_2^2 \]
\[ d_2^2 =1600-576=1024\]
\[ d_2 =\sqrt{1024}=32 cm\]
∴ Area of the rhombus \[=\frac{1}{2}(24 \times 32) = 384 {cm}^2\]
संबंधित प्रश्न
The floor of a building consists of 3000 tiles, which are rhombus shaped, and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor if the cost per m2 is ₹ 4.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. It the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
The area of a rhombus is 240 cm2 and one of the diagonal is 16 cm. Find another diagonal.
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs 4.
A rectangular grassy plot is 112 m long and 78 m broad. It has a gravel path 2.5 m wide all around it on the side. Find the area of the path and the cost of constructing it at Rs 4.50 per square metre.
The length of a side of a square field is 4 m. what will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonal is 2 m?
The area of a rhombus is 84 m2. If its perimeter is 40 m, then find its altitude.
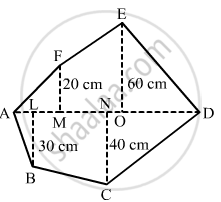
Find the area of the following regular hexagon.
Polygon ABCDE is divided in different parts as shown in figure. If AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and BF = 2 cm, CH = 3cm, EG = 2.5 cm. Then find the area of the polygon.
