Advertisements
Advertisements
प्रश्न
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2?
उत्तर
Base of a flooring tile that is in the shape of a parallelogram = b = 24 cm
Corresponding height = h = 10 cm
Now, in a parallelogram:
Area(A) = Base (b) x Height (h)
\[ \therefore\text{ Area of a tile }= 24 cm \times 10 cm = 240 {cm}^2 \]
Now, observe that the area of the floor is 1080 \[m^2 . \]
\[1080 m^2 = 1080 \times 1m \times 1m\]
\[ = 1080 \times 100 cm \times 100 cm (\text{ Because }1 m = 100 cm)\]
\[ = 1080 \times 100 \times 100 \times cm \times cm\]
\[ = 10800000 {\text{ cm }}^2 \]
∴ Number of required tiles =\[ \frac{10800000}{240} = 45000\]
APPEARS IN
संबंधित प्रश्न
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
The floor of a building consists of 3000 tiles, which are rhombus shaped, and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor if the cost per m2 is ₹ 4.
There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.

Find the area of this park using both ways. Can you suggest some other way of finding its area?
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Find the area of the field in the form of a rhombus, if the length of each side be 14 cm and the altitude be 16 cm.
A field in the form of a rhombus has each side of length 64 m and altitude 16 m. What is the side of a square field which has the same area as that of a rhombus?
Find the area of the following polygon, if AL = 10 cm, AM = 20 cm, AN = 50 cm, AO = 60 cm and AD = 90 cm.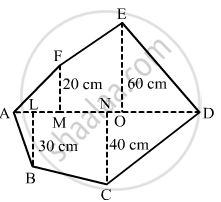
Polygon ABCDE is divided in different parts as shown in figure. If AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and BF = 2 cm, CH = 3cm, EG = 2.5 cm. Then find the area of the polygon.

