Question

There is a hexagon MNOPQR of side 5 cm. Aman and Ridhima divided it into two different ways. Find the area of this hexagon using both ways.

Answer 1

Aman’s method:

Since it is a hexagon so NQ divides the hexagon into two congruent trapeziums.

Now area of trapezium MNQR = `4 xx ((11 + 5))/2 = 2 xx 16 = 32` cm² 

So the area of hexagon MNOPQR = 2 × 32 = 64 cm².

 

Ridhima’s method:

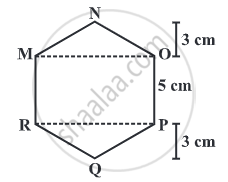
∆MNO and ∆RPQ are congruent triangles with an altitude of 3 cm.

Area of ∆MNO = `1/2 xx 8 xx 3` = 12 cm² = Area of ∆ RPQ

Area of rectangle MOPR = 8 × 5 = 40 cm².

Now, area of hexagon MNOPQR = 40 + 12 + 12 = 64 cm².