Advertisements
Advertisements
Question
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs 4.
Solution
Given:
The floor consist of 3000 rhombus shaped tiles .
The lengths of the diagonals of each tile are 45 cm and 30 cm.
∴Area of a rhombus shaped tile =\[ \frac{1}{2} \times (45 \times 30) = 675 {cm}^2 \]
∴ Area of the complete floor\[ = 3000 \times 675 = 2025000 {cm}^2 \]
Now, we need to convert this area into `m^2` because the rate of polishing is given as per `m^2`.
\[ \therefore 2025000 {cm}^2 = 2025000 \times cm \times cm\]
\[ = 2025000 \times \frac{1}{100} m \times \frac{1}{100} m\]
\[ = 202 . 5 m^2 \]
Now, the cost of polishing 1 `m^2` is Rs 4.
∴ Total cost of polishing the complete floor = 202 . 5 x 4 = 810
Thus, the total cost of polishing the floor is Rs 810.
APPEARS IN
RELATED QUESTIONS
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2?
The area of a rhombus is 240 cm2 and one of the diagonal is 16 cm. Find another diagonal.
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
Find the area of the field in the form of a rhombus, if the length of each side be 14 cm and the altitude be 16 cm.
In exchange of a square plot one of whose sides is 84 m, a man wants to buy a rectangular plot 144 m long and of the same area as of the square plot. Find the width of the rectangular plot.
A garden is in the form of a rhombus whose side is 30 metres and the corresponding altitude is 16 m. Find the cost of levelling the garden at the rate of Rs 2 per m2.
Find the area of the following polygon, if AL = 10 cm, AM = 20 cm, AN = 50 cm, AO = 60 cm and AD = 90 cm.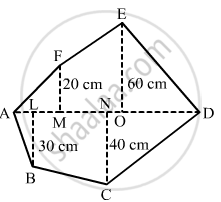
Find the area of the following regular hexagon.
