Advertisements
Advertisements
Question
The area of a rhombus is 240 cm2 and one of the diagonal is 16 cm. Find another diagonal.
Advertisements
Solution
Given:
Area of the rhombus = 240 cm
Length of one of its diagonals = 16 cm
We know that if the diagonals of a rhombus are `d_1` and `d_2` , then the area of the rhombus is given by:
Area \[= \frac{1}{2}( d_1 \times d_2 )\]
Putting the given values:
\[240 = \frac{1}{2}(16 \times d_2 )\]
\[240 \times 2 = 16 \times d_2 \]
This can be written as follows:
\[16 \times d_2 = 480\]
\[ d_2 = \frac{480}{16}\]
\[ d_2 = 30 cm\]
Thus, the length of the other diagonal of the rhombus is 30 cm.
RELATED QUESTIONS
The floor of a building consists of 3000 tiles, which are rhombus shaped, and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor if the cost per m2 is ₹ 4.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. It the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2?
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs 4.
A rectangular grassy plot is 112 m long and 78 m broad. It has a gravel path 2.5 m wide all around it on the side. Find the area of the path and the cost of constructing it at Rs 4.50 per square metre.
In exchange of a square plot one of whose sides is 84 m, a man wants to buy a rectangular plot 144 m long and of the same area as of the square plot. Find the width of the rectangular plot.
The area of a rhombus is equal to the area of a triangle whose base and the corresponding altitude are 24.8 cm and 16.5 cm respectively. If one of the diagonals of the rhombus is 22 cm, find the length of the other diagonal.
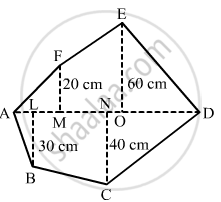
Find the area of the following regular hexagon.
