Advertisements
Advertisements
प्रश्न
The area of a rhombus is 240 cm2 and one of the diagonal is 16 cm. Find another diagonal.
Advertisements
उत्तर
Given:
Area of the rhombus = 240 cm
Length of one of its diagonals = 16 cm
We know that if the diagonals of a rhombus are `d_1` and `d_2` , then the area of the rhombus is given by:
Area \[= \frac{1}{2}( d_1 \times d_2 )\]
Putting the given values:
\[240 = \frac{1}{2}(16 \times d_2 )\]
\[240 \times 2 = 16 \times d_2 \]
This can be written as follows:
\[16 \times d_2 = 480\]
\[ d_2 = \frac{480}{16}\]
\[ d_2 = 30 cm\]
Thus, the length of the other diagonal of the rhombus is 30 cm.
संबंधित प्रश्न
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.
Find the area of this park using both ways. Can you suggest some other way of finding its area?
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
The cost of fencing a square field at 60 paise per metre is Rs 1200. Find the cost of reaping the field at the rate of 50 paise per 100 sq. metres.
A garden is in the form of a rhombus whose side is 30 metres and the corresponding altitude is 16 m. Find the cost of levelling the garden at the rate of Rs 2 per m2.
A field in the form of a rhombus has each side of length 64 m and altitude 16 m. What is the side of a square field which has the same area as that of a rhombus?
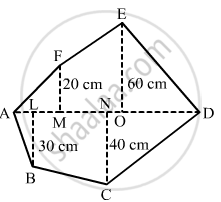
A regular hexagon is inscribed in a circle of radius r. The perimeter of the regular hexagon is ______.
