Advertisements
Advertisements
प्रश्न
The diameter of a wheel of a bus is 90 cm which makes 315 revolutions per minute. Determine its speed in kilometres per hour. [Use π = 22/7]
उत्तर
It is given that the diameter of the wheel is 90 cm.
∴ Radius of the circular wheel, r \[= \frac{90}{2} = 45 cm . \]
∴ Perimeter of the wheel \[= 2 \times \pi \times r = 2 \times \frac{22}{7} \times 45 = 282 . 857 cm\]
It means the wheel travels 282 . 857 cm in a revolution.
Now, it makes 315 revolutions per minute.
∴ Distance travelled by the wheel in one minute \[= 315 \times 282 . 857 = 89100 cm\]
∴ Speed = 89100 cm per minute \[= \frac{89100 cm}{1 \text{ minute }}\]
Now, we need to convert it into kilometers per hour.
\[ \therefore \frac{89100 cm}{1\text{ minute }} = \frac{89100 \times \frac{1}{100000}\text{ kilometer }}{\frac{1}{60}\text{ hour }}\]
\[ = \frac{89100}{100000} \times \frac{60}{1} \times \frac{\text{ kilometer }}{\text{ hour }}\]
= 53 . 46 kilometers per hour
APPEARS IN
संबंधित प्रश्न
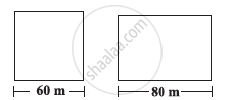
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the corners).
A rectangular piece is 20 m long and 15 m wide. From its four corners, quadrants of radii 3.5 m have been cut. Find the area of the remaining part.
The inside perimeter of a running track (shown in Fig. 20.24) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.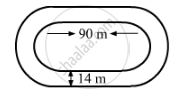
Find the area of Fig. 20.25, in square cm, correct to one place of decimal. (Take π = 22/7)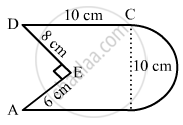
The length and breadth of a rectangular field are in the ratio 7 : 4. If its perimeter is 440 m, find its length and breadth. Also, find the cost of fencing it @ ₹150 per m.
The length and the breadth of a rectangular plot are 135 m and 65 m. Find, its perimeter and the cost of fencing it at the rate of ₹60 per m.
The length and breadth of the rectangular piece of land area in the ratio of 5 : 3. If the total cost of fencing it at the rate of ₹48 per metre is ₹19,200, find its length and breadth.
A wire is in the shape of square of side 20 cm. If the wire is bent into a rectangle of length 24 cm, find its breadth.
The area of a parallelogram is 60 cm2 and one of its altitudes is 5 cm. The length of its corresponding side is ______.
