Topics
Rational Numbers
- Rational Numbers
- Closure Property of Rational Numbers
- Commutative Property of Rational Numbers
- Associative Property of Rational Numbers
- Distributive Property of Multiplication Over Addition for Rational Numbers
- Identity of Addition and Multiplication of Rational Numbers
- Negative Or Additive Inverse of Rational Numbers
- Concept of Reciprocal or Multiplicative Inverse
- Rational Numbers on a Number Line
- Rational Numbers Between Two Rational Numbers
Linear Equations in One Variable
- Variable of Equation
- Concept of Equation
- Expressions with Variables
- Balancing an Equation
- The Solution of an Equation
- Linear Equation in One Variable
- Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side
- Some Applications Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side
- Solving Equations Having the Variable on Both Sides
- Some More Applications on the Basis of Solving Equations Having the Variable on Both Sides
- Reducing Equations to Simpler Form
- Equations Reducible to the Linear Form
Understanding Quadrilaterals
- Concept of Curves
- Different Types of Curves - Closed Curve, Open Curve, Simple Curve.
- Concept of Polygons
- Classification of Polygons
- Properties of a Quadrilateral
- Interior Angles of a Polygon
- Exterior Angles of a Polygon and Its Property
- Concept of Quadrilaterals
- Properties of Trapezium
- Properties of Kite
- Properties of a Parallelogram
- Properties of Rhombus
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Property: The adjacent angles in a parallelogram are supplementary.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Property: The diagonals of a rhombus are perpendicular bisectors of one another.
- Property: The Diagonals of a Rectangle Are of Equal Length.
- Properties of Rectangle
- Properties of a Square
- Property: The diagonals of a square are perpendicular bisectors of each other.
Practical Geometry
- Introduction to Geometric Tool
- Constructing a Quadrilateral When the Lengths of Four Sides and a Diagonal Are Given
- Constructing a Quadrilateral When Two Diagonals and Three Sides Are Given
- Constructing a Quadrilateral When Two Adjacent Sides and Three Angles Are Known
- Constructing a Quadrilateral When Three Sides and Two Included Angles Are Given
- Some Special Cases
Data Handling
- Concept of Data Handling
- Interpretation of a Pictograph
- Interpretation of Bar Graphs
- Drawing a Bar Graph
- Interpretation of a Double Bar Graph
- Drawing a Double Bar Graph
- Organisation of Data
- Frequency Distribution Table
- Graphical Representation of Data as Histograms
- Concept of Pie Graph (Or a Circle-graph)
- Interpretation of Pie Diagram
- Chance and Probability - Chance
- Basic Ideas of Probability
Squares and Square Roots
- Concept of Square Number
- Properties of Square Numbers
- Some More Interesting Patterns of Square Number
- Finding the Square of a Number
- Concept of Square Roots
- Finding Square Root Through Repeated Subtraction
- Finding Square Root Through Prime Factorisation
- Finding Square Root by Division Method
- Square Root of Decimal Numbers
- Estimating Square Root
Cubes and Cube Roots
Comparing Quantities
- Concept of Ratio
- Basic Concept of Percentage
- Increase Or Decrease as Percent
- Concept of Discount
- Estimation in Percentages
- Basic Concepts of Profit and Loss
- Sales Tax, Value Added Tax, and Good and Services Tax
- Calculation of Interest
- Concept of Compound Interest
- Deducing a Formula for Compound Interest
- Rate Compounded Annually Or Half Yearly (Semi Annually)
- Applications of Compound Interest Formula
Algebraic Expressions and Identities
- Algebraic Expressions
- Terms, Factors and Coefficients of Expression
- Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials
- Like and Unlike Terms
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Multiplication of Algebraic Expressions
- Multiplying Monomial by Monomials
- Multiplying a Monomial by a Binomial
- Multiplying a Monomial by a Trinomial
- Multiplying a Binomial by a Binomial
- Multiplying a Binomial by a Trinomial
- Concept of Identity
- Expansion of (a + b)2 = a2 + 2ab + b2
- Expansion of (a - b)2 = a2 - 2ab + b2
- Expansion of (a + b)(a - b) = a2-b2
- Expansion of (x + a)(x + b)
Mensuration
Visualizing Solid Shapes
Exponents and Powers
Direct and Inverse Proportions
Factorization
- Factors and Multiples
- Factorising Algebraic Expressions
- Factorisation by Taking Out Common Factors
- Factorisation by Regrouping Terms
- Factorisation Using Identities
- Factors of the Form (x + a)(x + b)
- Dividing a Monomial by a Monomial
- Dividing a Polynomial by a Monomial
- Dividing a Polynomial by a Polynomial
- Concept of Find the Error
Introduction to Graphs
- Concept of Bar Graph
- Interpretation of Bar Graphs
- Drawing a Bar Graph
- Concept of Double Bar Graph
- Interpretation of a Double Bar Graph
- Drawing a Double Bar Graph
- Concept of Pie Graph (Or a Circle-graph)
- Graphical Representation of Data as Histograms
- Concept of a Line Graph
- Linear Graphs
- Some Application of Linear Graphs
Playing with Numbers
- Location of a Point
- Coordinates
Definition
- Linear graph: A line graph which is a whole unbroken line is called a linear graph.
- Cartesian system: The system used to describe the position of a point in a plane is called the Cartesian system.
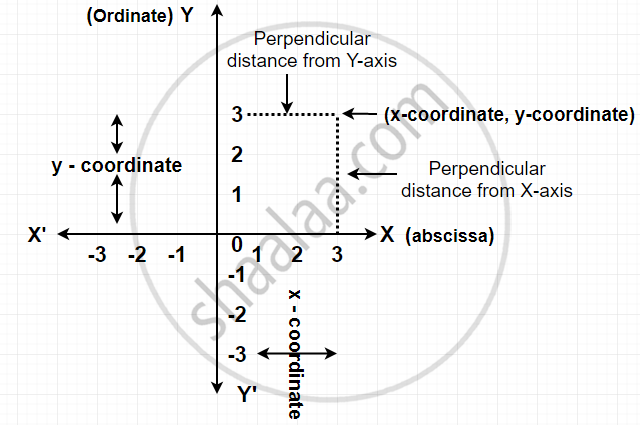
- Origin: The point of intersection of x and y lines is called the origin.
- Abscissa: X-coordinate tells how many units to move right or left. It is also called the Abscissa.
- Ordinate: Y-coordinate tells how many units to move up or down. It is also called the Ordinate.
- Cartesian Coordinate: X-coordinate and y-coordinate taken together are called cartesian coordinates or coordinates of a point and denoted by (x, y).
- Ordered pair: The x-coordinate comes first, and after this y-coordinate comes. (x, y) is called an ordered pair.
Notes
Linear Graphs:
A line graph which is a whole unbroken line is called a linear graph.
1. Location of a point:
-
The system used to describe the position of a point in a plane is called the Cartesian system.
-
In the Cartesian system, there are two perpendicular directed straight lines XX’ and YY’ which intersect at point 0, then line XX’ will be a horizontal line and YY’ will be a vertical line.
-
The point of intersection of these lines is called origin and it is denoted by O. In other words, the point from which distances are marked is called an origin.
-
The horizontal line XOX’ is called X-axis and the vertical line YOY’ is called Y-axis.
-
Directions OX and OY are called the positive directions of the X-axis and Y-axis, respectively, and directions OX’ and OY’ are called the negative directions of the X-axis and Y-axis, respectively.
2. Coordinates:
-
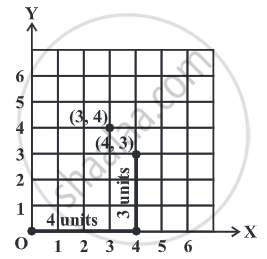
For fixing a point on the graph sheet we need, x-coordinate and y-coordinate.
-
x-coordinate tells how many units to move right or left. It is also called the Abscissa.
-
y-coordinate tells how many units to move up or down. It is also called the Ordinate.
-
x-coordinate and y-coordinate taken together are called cartesian coordinates or coordinates of a point and denoted by (x, y). Here, the x-coordinate comes first, and after this y-coordinate comes. (x, y) is called an ordered pair.
Example
Plot the point (4, 3) on a graph sheet. Is it the same as the point (3, 4)?
The points (3, 4) and (4, 3) are two different points.
Example
From Fig, choose the letter(s) that indicate the location of the points given below:
(i) (2, 1)
(ii) (0, 5)
(iii) (2, 0)
Also, write
(iv) The coordinates of A.
(v) The coordinates of F.
(i) (2, 1) is the point E.
(ii) (0, 5) is the point B.
(iii) (2, 0) is the point G.
(iv) Point A is (4, 5)
(v) F is (5.5, 0)
Example
Plot the following points and verify if they lie on a line. If they lie on a line, name it.
(0, 2), (0, 5), (0, 6), (0, 3.5)
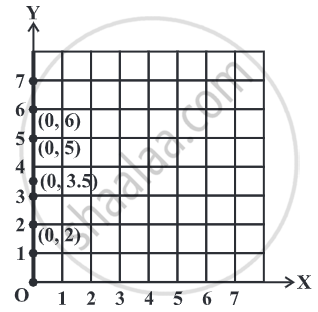
These lie on a line. The line is the y-axis.
Example
Plot the following points and verify if they lie on a line. If they lie on a line, name it.
A (1, 1), B (1, 2), C (1, 3), D (1, 4)
These lie on a line. The line is AD.
It is parallel to the y-axis
Example
Plot the following points and verify if they lie on a line. If they lie on a line, name it.
K (1, 3), L (2, 3), M (3, 3), N (4, 3)
These lie on a line. We can name it as KL or KM or MN etc. It is parallel to the x-axis.
Example
Plot the following points and verify if they lie on a line. If they lie on a line, name it.
W(2, 6), X (3, 5), Y(5, 3), Z (6, 2)
These lie on a line. We can name it as XY or WY or YZ etc.
If you would like to contribute notes or other learning material, please submit them using the button below.
Shaalaa.com | How to Plot points on a graph
to track your progress
Series: Linear Graphs
0%
Related QuestionsVIEW ALL [102]
The following table gives the growth chart of a child.
| Height (in cm) | 75 | 90 | 110 | 120 | 130 |
| Age (in years) | 2 | 4 | 6 | 8 | 10 |
Draw a line graph for the table and answer the questions that follow.
- What is the height at the age of 5 years?
- How much taller was the child at the age of 10 than at the age of 6?
- Between which two consecutive periods did the child grow more faster?
