Topics
Integers
- Concept for Natural Numbers
- Concept for Whole Numbers
- Negative and Positive Numbers
- Concept of Integers
- Representation of Integers on the Number Line
- Concept for Ordering of Integers
- Addition of Integers
- Subtraction of Integers
- Properties of Addition and Subtraction of Integers
- Multiplication of a Positive and a Negative Integers
- Multiplication of Two Negative Integers
- Product of Three Or More Negative Integers
- Closure Property of Multiplication of Integers
- Commutative Property of Multiplication of Integers
- Multiplication of Integers with Zero
- Multiplicative Identity of Integers
- Associative Property of Multiplication of Integers
- Distributive Property of Multiplication of Integers
- Making Multiplication Easier of Integers
- Division of Integers
- Properties of Division of Integers
Fractions and Decimals
- Concept of Fractions
- Fraction and its Types
- Concept of Proper Fractions
- Improper Fraction and Mixed Fraction
- Concept of Equivalent Fractions
- Like and Unlike Fraction
- Comparing Fractions
- Addition of Fraction
- Subtraction of Fraction
- Multiplication of a Fraction by a Whole Number
- Fraction as an Operator 'Of'
- Multiplication of Fraction
- Division of Fractions
- Concept of Reciprocal or Multiplicative Inverse
- Problems Based on Fraction
- The Decimal Number System
- Comparing Decimal Numbers
- Addition of Decimal Fraction
- Subtraction of Decimal Numbers
- Multiplication of Decimal Fractions
- Multiplication of Decimal Numbers by 10, 100 and 1000
- Division of Decimal Numbers by 10, 100 and 1000
- Division of Decimal Fractions
- Division of a Decimal Number by Another Decimal Number
- Problems Based on Decimal Numbers
Data Handling
Simple Equations
Lines and Angles
- Concept of Points
- Concept of Line
- Concept of Line Segment
- Concept of Angle
- Complementary Angles
- Supplementary Angles
- Concept of Angle
- Concept of Linear Pair
- Concept of Vertically Opposite Angles
- Concept of Intersecting Lines
- Introduction to Parallel Lines
- Pairs of Lines - Transversal
- Pairs of Lines - Angles Made by a Transversal
- Pairs of Lines - Transversal of Parallel Lines
The Triangle and Its Properties
- Concept of Triangles
- Classification of Triangles (On the Basis of Sides, and of Angles)
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- 3. Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- 3. Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- Median of a Triangle
- Altitudes of a Triangle
- Exterior Angle of a Triangle and Its Property
- Angle Sum Property of a Triangle
- Some Special Types of Triangles - Equilateral and Isosceles Triangles
- Sum of the Lengths of Two Sides of a Triangle
- Right-angled Triangles and Pythagoras Property
Comparing Quantities
- Concept of Ratio
- Concept of Equivalent Ratios
- Concept of Proportion
- Concept of Unitary Method
- Basic Concept of Percentage
- Conversion between Percentage and Fraction
- Converting Decimals to Percentage
- Conversion between Percentage and Fraction
- Converting Percentages to Decimals
- Estimation in Percentages
- Interpreting Percentages
- Converting Percentages to “How Many”
- Ratios to Percents
- Increase Or Decrease as Percent
- Basic Concepts of Profit and Loss
- Profit or Loss as a Percentage
- Calculation of Interest
Congruence of Triangles
Rational Numbers
- Rational Numbers
- Equivalent Rational Number
- Positive and Negative Rational Numbers
- Rational Numbers on a Number Line
- Rational Numbers in Standard Form
- Comparison of Rational Numbers
- Rational Numbers Between Two Rational Numbers
- Addition of Rational Number
- Subtraction of Rational Number
- Multiplication of Rational Numbers
- Division of Rational Numbers
Perimeter and Area
- Mensuration
- Concept of Perimeter
- Perimeter of a Rectangle
- Perimeter of Squares
- Perimeter of Triangles
- Perimeter of Polygon
- Concept of Area
- Area of Square
- Area of Rectangle
- Triangles as Parts of Rectangles and Square
- Generalising for Other Congruent Parts of Rectangles
- Area of a Parallelogram
- Area of a Triangle
- Circumference of a Circle
- Area of Circle
- Conversion of Units
- Problems based on Perimeter and Area
Algebraic Expressions
- Algebraic Expressions
- Terms, Factors and Coefficients of Expression
- Like and Unlike Terms
- Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Evaluation of Algebraic Expressions by Substituting a Value for the Variable.
- Use of Variables in Common Rules
Practical Geometry
- Construction of a Line Parallel to a Given Line, Through a Point Not on the Line
- Construction of Triangles
- Constructing a Triangle When the Length of Its Three Sides Are Known (SSS Criterion)
- Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle Between Them Are Known. (SAS Criterion)
- Constructing a Triangle When the Measures of Two of Its Angles and the Length of the Side Included Between Them is Given. (ASA Criterion)
- Constructing a Right-angled Triangle When the Length of One Leg and Its Hypotenuse Are Given (RHS Criterion)
Exponents and Powers
- Concept of Exponents
- Multiplying Powers with the Same Base
- Dividing Powers with the Same Base
- Taking Power of a Power
- Multiplying Powers with Different Base and Same Exponents
- Dividing Powers with Different Base and Same Exponents
- Numbers with Exponent Zero, One, Negative Exponents
- Miscellaneous Examples Using the Laws of Exponents
- Decimal Number System Using Exponents and Powers
- Crores
Symmetry
Visualizing Solid Shapes
Notes
Multiplication of Decimal Numbers:
Let us now learn the multiplication of two decimal numbers.
1) Find 0.1 × 0.1.
Now, 0.1 = `1/10. "So", 0.1 xx 0.1 = 1/10 xx 1/10 = (1xx1)/(10xx10) = 1/100 = 0.01.`
Let us see it’s a pictorial representation,
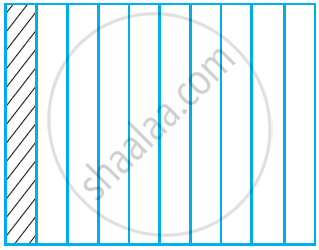
The fraction `1/10` represents 1 part out of 10 equal parts. The shaded part in the picture represents `1/10`.
We know that, `1/10 xx 1/10 "means" 1/10 "of" 1/10`.
So, divide this `1/10`th part into 10 equal parts and take one part out of it.
Thus, we have,
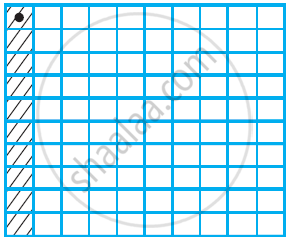
The dotted square is one part out of 10 of the `1/10`th part. That is, it represents `1/10 xx 1/10 "or" 0.1 xx 0.1`.
There are 100 small squares. So the dotted square represents one out of 100 or 0.01. Hence, 0.1 × 0.1 = 0.01.
2) Find 0.2 × 0.3.
We have, 0.2 × 0.3 = `2/10 xx 3/10`
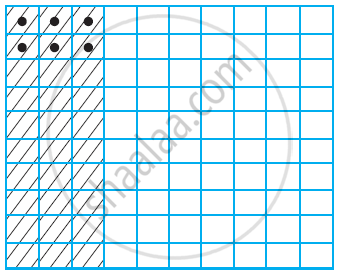
As we did for `1/10 xx 1/10`, let us divide the square into 10 equal parts and take three parts out of it, to get `3/10`. Again divide each of these three equal parts into 10 equal parts and take two from each.
We get `2/10 xx 3/10`.
The dotted squares represent `2/10 xx 3/10` or 0.2 × 0.3.
Since there are 6 dotted squares out of 100, so they also represent 0.06.
Thus, 0.2 × 0.3 = 0.06.
Example
Multiply 0.1 × 0.1
| 0.1 | |
| × | 0.1 |
| 0 1 | |
| + | 0 0 0 |
| 0 . 0 1 |
Example
Multiply 2.3 × 3.8
| 2.3 | |
| × | 3.8 |
| 184 | |
| + | 690 |
| 8.74 |
Example
Multiply 1.25 × 3.78
| 1.25 | |
| × | 3.78 |
| 1000 | |
| + | 8750 |
| + | 37500 |
| 4.7250 |
Example
The side of an equilateral triangle is 3.5 cm. Find its perimeter.
All the sides of an equilateral triangle are equal.
So, length of each side = 3.5 cm
Thus, perimeter = 3 × 3.5 cm = 10.5 cm
Example
The length of a rectangle is 7.1 cm and its breadth is 2.5 cm. What is the area of the rectangle?
Length of the rectangle = 7.1 cm
Breadth of the rectangle = 2.5 cm
Therefore, area of the rectangle = 7.1 × 2.5 cm2 = 17.75 cm2
