Advertisements
Advertisements
Question
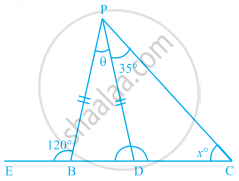
In the given figure, PB = PD. The value of x is ______.
Options
85°
90°
25°
35°
Solution
In the given figure, PB = PD. The value of x is 25°.
Explanation:

∠PBE = ∠PDB + ∠BPD ......[Exterior angle property]
⇒ 120° = ∠PDB + θ ………….. (i)
Now, in ΔPBD, ∠PBD + ∠BPD + ∠PDB = 180° ......[Angle sum property]
⇒ ∠PBD + θ + ∠PDB = 180°
⇒ ∠PBD = 180° – 120° = 60° ......[Using (i)]
And PB = PD ......(Given)
∵ ∠PDB = ∠PBD = 60° ......(ii)
Now, in ΔPDC,
∠PDB = ∠DCP + ∠DPC ......[Exterior angle property]
⇒ 60° = x + 35° ......[Using (ii)] [∵ ∠DCP = x, ∠DPC = 35° (given)]
⇒ x = 60° – 35° = 25°
APPEARS IN
RELATED QUESTIONS
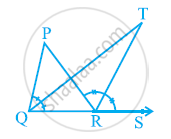
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
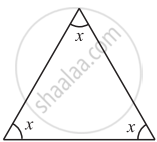
Find the value of the unknown x in the following diagram:
In the given figure find m∠P.
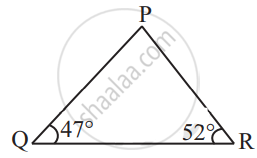
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is ______.
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
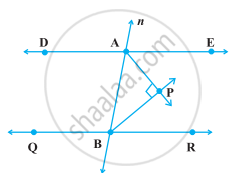
Prove that through a given point, we can draw only one perpendicular to a given line.
[Hint: Use proof by contradiction].
It is possible to have a triangle in which each angle is greater than 60°.
In the given figure, find the value of x.
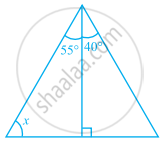
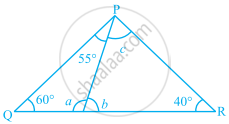
In the given figure, find the values of a, b and c