Advertisements
Advertisements
Question
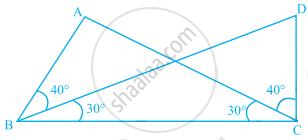
In the given figure ray AZ bisects ∠BAD and ∠DCB, prove that ∆BAC ≅ ∆DAC
Solution
In ∆BAC and ∆DAC
∠BAC = ∠DAC ...[Given `bar("AZ")` bisects ∠BAD]
∠BCA = ∠DCA ...[`bar("AZ")` bisects ∠DCB]
AC = AC ...[∵ common side]
∴ Here AC is the included side of the angles
By ASA criterior, ∆BAC ≅ ∆DAC.
APPEARS IN
RELATED QUESTIONS
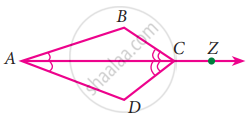
In Fig, can you use the ASA congruence rule and conclude that ∆AOC ≅ ∆BOD?

Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent:
In the given figure, AD = CD and AB = CB. Identify the other three pairs that are equal
In the given figure ray AZ bisects ∠BAD and ∠DCB, prove that AB = AD

If hypotenuse and an acute angle of one right triangle are equal to the hypotenuse and an acute angle of another right triangle, then the triangles are congruent.
In the given figure, AD ⊥ BC and AD is the bisector of angle BAC. Then, ∆ABD ≅ ∆ACD by RHS.
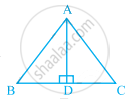
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
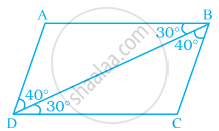
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
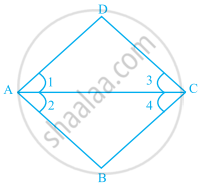
In the given figure, ∠1 = ∠2 and ∠3 = ∠4.
- Is ∆ADC ≅ ∆ABC? Why ?
- Show that AD = AB and CD = CB.
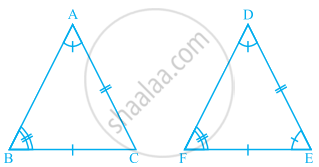
Observe the given figure and state the three pairs of equal parts in triangles ABC and DBC.
- Is ∆ABC ≅ ∆DCB? Why?
- Is AB = DC? Why?
- Is AC = DB? Why?