Advertisements
Advertisements
Question
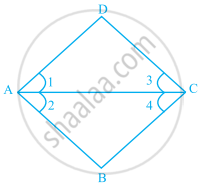
In the given figure, ∠1 = ∠2 and ∠3 = ∠4.
- Is ∆ADC ≅ ∆ABC? Why ?
- Show that AD = AB and CD = CB.
Solution
i. In ∆ADC and ∆ABC,
∠1 = ∠2 ......(Given)
AC = AC ......(Common)
∠3 = ∠4 ......(Given)
∴ ∆ADC = ∆ABC ......(ASA criterion)
ii. By using (i) part, we get
AD = AB ......(By C.P.C.T.)
And CD = CB ......(By C.P.C.T.)
APPEARS IN
RELATED QUESTIONS
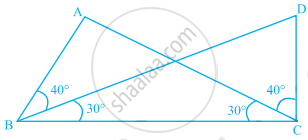
In Fig, can you use the ASA congruence rule and conclude that ∆AOC ≅ ∆BOD?

Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by the ASA congruence rule. In the case of congruence, write it in symbolic form.
∆DEF, ∠D = 60º, ∠F = 80º, DF = 6 cm.
∆PQR, ∠Q = 60º, ∠R = 80º, QP = 6 cm.
In the figure, ∠TMA ≡∠IAM and ∠TAM ≡ ∠IMA. P is the midpoint of MI and N is the midpoint of AI. Prove that ΔPIN ~ ΔATM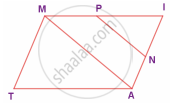
To conclude the congruency of triangles, mark the required information in the following figure with reference to the given congruency criterion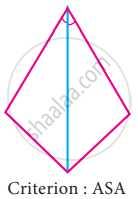
To conclude the congruency of triangles, mark the required information in the following figure with reference to the given congruency criterion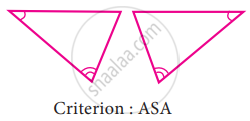
In the given figure, AD = CD and AB = CB. Identify the other three pairs that are equal
In the given figure ray AZ bisects ∠BAD and ∠DCB, prove that ∆BAC ≅ ∆DAC
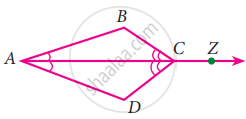
In the given figure, Δ______ ≅ ΔPQR.
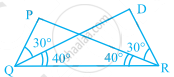
In the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
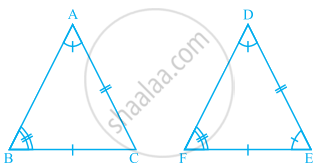
Observe the given figure and state the three pairs of equal parts in triangles ABC and DBC.
- Is ∆ABC ≅ ∆DCB? Why?
- Is AB = DC? Why?
- Is AC = DB? Why?