Advertisements
Advertisements
Question
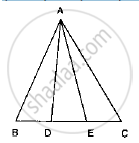
In the following figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you answer the question that you have left in the ’Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
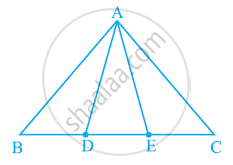
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
Solution
Let us draw a line segment AM ⊥ BC.
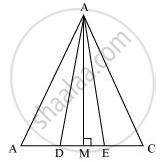
We know that,
Area of a triangle = 1/2 × Base × Altitude
`"Area "(triangleADE)=1/2xxDExxAM`
`"Area "(triangleABD)=1/2xxBDxxAM`
`"Area "(triangleAEC)=1/2xxECxxAM`
It is given that DE = BD = EC
`⇒ 1/2xxDExxAM=1/2xxBDxxAM=1/2xxECxxAM`
⇒ Area (ΔADE) = Area (ΔABD) = Area (ΔAEC)
It can be observed that Budhia has divided her field into 3 equal parts.
APPEARS IN
RELATED QUESTIONS
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
In the given figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
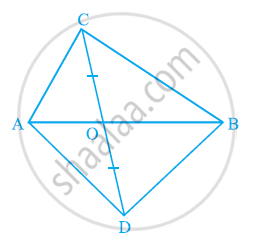
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:-
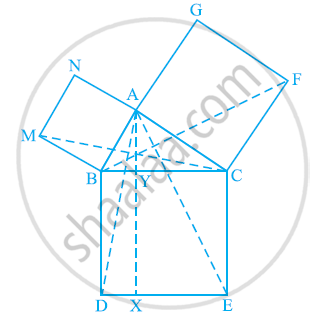
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
In the following figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = `1/2` ar (EFGD).
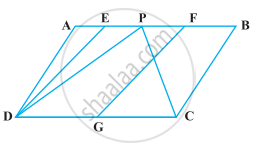
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)