Advertisements
Advertisements
प्रश्न
In the following figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you answer the question that you have left in the ’Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
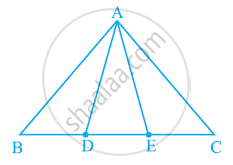
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
उत्तर
Let us draw a line segment AM ⊥ BC.
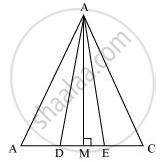
We know that,
Area of a triangle = 1/2 × Base × Altitude
`"Area "(triangleADE)=1/2xxDExxAM`
`"Area "(triangleABD)=1/2xxBDxxAM`
`"Area "(triangleAEC)=1/2xxECxxAM`
It is given that DE = BD = EC
`⇒ 1/2xxDExxAM=1/2xxBDxxAM=1/2xxECxxAM`
⇒ Area (ΔADE) = Area (ΔABD) = Area (ΔAEC)
It can be observed that Budhia has divided her field into 3 equal parts.
APPEARS IN
संबंधित प्रश्न
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
In a ΔABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point
of AP. Prove that :
(1) ar (Δ PBQ) = ar (Δ ARC)
(2) ar (Δ PRQ) =`1/2`ar (Δ ARC)
(3) ar (Δ RQC) =`3/8` ar (Δ ABC) .
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔBEF)
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)
In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).