Advertisements
Advertisements
प्रश्न
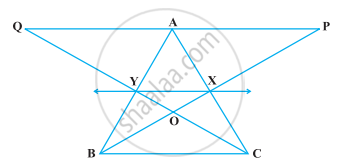
In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).
उत्तर
Given: X and Y are the mid-points of AC and AB respectively. Also, QP || BC and CYQ, BXP are straight lines.
To prove: ar (ΔABP) = ar (ΔACQ)
Proof: Since, X and Y are the mid-points of AC and AB respectively.
So, XY || BC
We know that, triangles on the same base and between the same parallels are equal in area.
Here, ΔBYC and ΔBXC lie on same base BC and between the same parallels BC and XY.
So, ar (ΔBYC) = ar (ΔBXC)
On subtracting ar (ΔBOC) from both sides, we get
ar (ΔBYC) – ar (ΔBOC) = ar (ΔBXC) – ar (ΔBOC)
=» ar (ΔBOY) = ar (ΔCOX)
On adding ar (ΔXOY) both sides, we get
ar (ΔSOY) + ar (ΔXOY) = ar (ΔCOX) + ar (ΔXOY)
⇒ ar (ΔBYX) = ar (ΔCXY) ...(i)
Hence, we observe that quadrilaterals XYAP and YXAQ are on the same base XY and between the same parallels XY and PQ.
ar (XYAP) = ar (YXAQ) ...(ii)
On adding equations (i) and (ii), we get
ar (ΔBYX) + ar (XYAP) = ar (ΔCXY) + ar (YXAQ)
⇒ ar (ΔABP) = ar (ΔACQ)
Hence proved.
APPEARS IN
संबंधित प्रश्न
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 1/4ar (ABC).
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
[Hint: Join CX.]
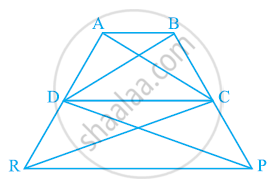
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar(PRQ) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
In a ΔABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point
of AP. Prove that :
(1) ar (Δ PBQ) = ar (Δ ARC)
(2) ar (Δ PRQ) =`1/2`ar (Δ ARC)
(3) ar (Δ RQC) =`3/8` ar (Δ ABC) .
In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid-point of
BC. AE intersects BC in F. Prove that
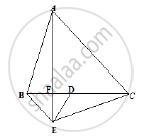
(1) ar (Δ BDE) = `1/2` ar (ΔABC)
(2) Area ( ΔBDE) `= 1/2 ` ar (ΔBAE)
(3) ar (BEF) = ar (ΔAFD)
(4) area (Δ ABC) = 2 area (ΔBEC)
(5) ar (ΔFED) `= 1/8` ar (ΔAFC)
(6) ar (Δ BFE) = 2 ar (ΔEFD)
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ASR = 90 cm2.
In ∆ABC, if L and M are the points on AB and AC, respectively such that LM || BC. Prove that ar (LOB) = ar (MOC)
If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
