Advertisements
Advertisements
प्रश्न
In a ΔABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point
of AP. Prove that :
(1) ar (Δ PBQ) = ar (Δ ARC)
(2) ar (Δ PRQ) =`1/2`ar (Δ ARC)
(3) ar (Δ RQC) =`3/8` ar (Δ ABC) .
उत्तर
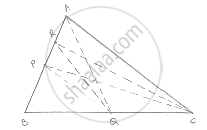
(1) We know that each median of a Δle divides it into two triangles of equal area
Since, OR is a median of ΔCAP
∴ ar (ΔCRA) = `1/2` ar (ΔCAP) ....... (1)
Also, CPis a median of ΔCAB
∴ ar ( ΔCAP) ar (ΔCPB) ....... (2)
From (1) and (2) we get
∴ area (Δ ARC ) = `1/2 ar (CPB)` ....... (3)
PQ is the median of ΔPBC
∴ area( Δ CPB) = 2area (Δ PBQ) ......... (4)
From (3) and (4) we get
∴ area (Δ ARC) = area (PBQ) ....... (5)
(2) Since QP and QR medians of s QAB and QAP respectively.
∴ ar (ΔQAP) = area (ΔPBQ) ............ (6)
And area (ΔQAP) = 2ar (QRP) ......... (7)
From (6) and (7) we have
Area (ΔPRQ) = `1/2` ar (ΔPBQ) ......... (8)
From (5) and (8) we get
Area (ΔPRQ) = `1/2` area (ΔARC)
(3) Since, ∠R is a median of ΔCAP
∴ area (ΔARC) = `1/2` ar (ΔCAP)
`= 1/2 xx1/2[ ar (ABC)]`
= `1/4` area (ABC)
Since RQ is a median of ΔRBC
∴ ar (ΔRQC) =`1/2` ar (Δ RBC)
= `1/2`[ ar (ΔABC)- ar (ARC) ]
= `1/2`[ar (ΔABC) - `1/4`(Δ ABC )]
= `3/8`(Δ ABC)
APPEARS IN
संबंधित प्रश्न
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid-point of
BC. AE intersects BC in F. Prove that
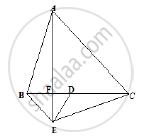
(1) ar (Δ BDE) = `1/2` ar (ΔABC)
(2) Area ( ΔBDE) `= 1/2 ` ar (ΔBAE)
(3) ar (BEF) = ar (ΔAFD)
(4) area (Δ ABC) = 2 area (ΔBEC)
(5) ar (ΔFED) `= 1/8` ar (ΔAFC)
(6) ar (Δ BFE) = 2 ar (ΔEFD)
ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2, then ar (ABC) = 24 cm2.
PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ASR = 90 cm2.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = `1/4` ar (ABC).
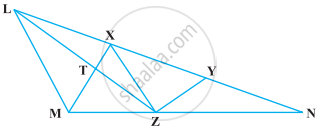
X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (See figure). Prove that ar (LZY) = ar (MZYX)
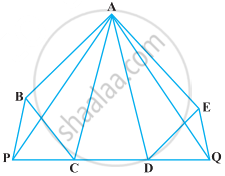
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)
If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
