Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
उत्तर
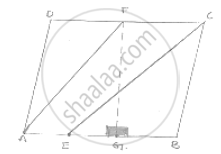
Construction: Draw FG ⊥ AB
Proof: We have
BE = 2EA and DF = 2 FC
⇒ AB - AE = 2EA and DC - FC = 2FC
⇒ AB = 3EA and DC = 3FC
⇒ AE = `1/2` AB and FC = ` 1/3` CD .......... (1)
But AB = DC
Then, AE = DC [opposite sides of ||gm]
Then, AE = FC
Thus, AE = FC and AE || FC.
Then, AECF is a parallelogram
Now ar (||gm = AECF) = AE × FG
⇒ ar (||gm =AECF) =`1/3 ABxx FG ` form ....... (1)
⇒ 3ar (||gm =AECF) = AB × FG ........(2)
and area (||gm =ABCD) = AB × FG ........... (3)
Compare equation (2) and (3)
⇒ 3 ar (||gm =AECF) = area (||gm =ABCD)
⇒ area (||gm =AECF) = `1/3` area (||gm =ABCD)
APPEARS IN
संबंधित प्रश्न
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
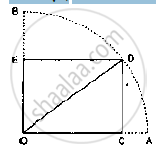
In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If
OE = 2√5, find the area of the rectangle.
The median of a triangle divides it into two ______.
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
Find the area of a rectangle whose length = 24 cm breadth =180 mm
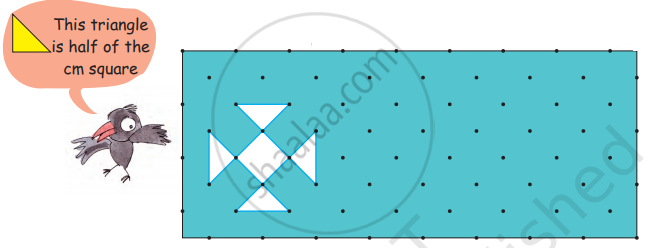
So the area of piece A = ________ square cm
How many tiles like the triangle given here will fit in the white design?
Area of design = ________ square cm
Find all the possible dimensions (in natural numbers) of a rectangle with a perimeter 36 cm and find their areas.
Find the area of the following figure by counting squares:
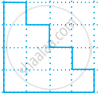
Find the area of the following figure by counting squares:

