Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
उत्तर
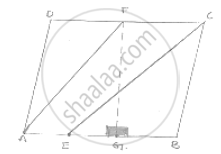
Construction: Draw FG ⊥ AB
Proof: We have
BE = 2EA and DF = 2 FC
⇒ AB - AE = 2EA and DC - FC = 2FC
⇒ AB = 3EA and DC = 3FC
⇒ AE = `1/2` AB and FC = ` 1/3` CD .......... (1)
But AB = DC
Then, AE = DC [opposite sides of ||gm]
Then, AE = FC
Thus, AE = FC and AE || FC.
Then, AECF is a parallelogram
Now ar (||gm = AECF) = AE × FG
⇒ ar (||gm =AECF) =`1/3 ABxx FG ` form ....... (1)
⇒ 3ar (||gm =AECF) = AB × FG ........(2)
and area (||gm =ABCD) = AB × FG ........... (3)
Compare equation (2) and (3)
⇒ 3 ar (||gm =AECF) = area (||gm =ABCD)
⇒ area (||gm =AECF) = `1/3` area (||gm =ABCD)
APPEARS IN
संबंधित प्रश्न
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove
that: (1) ar (ΔADO) = ar (ΔCDO) (2) ar (ΔABP) = ar (ΔCBP)
P is any point on base BC of ΔABC and D is the mid-point of BC. DE is drawn parallel toPA to meet AC at E. If ar (ΔABC) = 12 cm2, then find area of ΔEPC.
Two parallelograms are on the same base and between the same parallels. The ratio of their areas is
The median of a triangle divides it into two ______.
A floor is 40 m long and 15 m broad. It is covered with tiles, each measuring 60 cm by 50 cm. Find the number of tiles required to cover the floor.
Find the area of a rectangle whose length = 24 cm breadth =180 mm
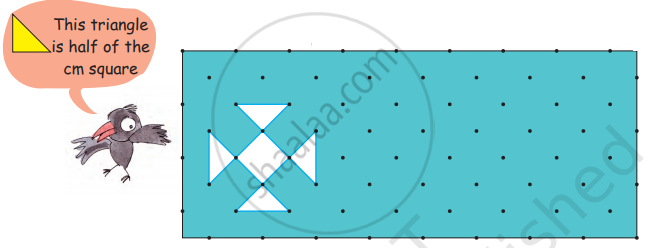
How many tiles like the triangle given here will fit in the white design?
Area of design = ________ square cm
The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar. Cheggu was happy. He took 100 meters of wire and tried to make different rectangles.
He made a 10 m × 40 m rectangle. Its area was 400 square meters. So he next made a 30 m × 20 m rectangle.
- What is its area? Is it more than the first rectangle?
Find the area of the following figure by counting squares:

