Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove
that: (1) ar (ΔADO) = ar (ΔCDO) (2) ar (ΔABP) = ar (ΔCBP)
उत्तर
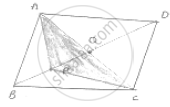
Given that ABCD is a parallelogram
To prove: (1) ar (ΔADO) = ar (ΔCDO)
(2) ar ( ΔABP) = ar (ΔCBP)
Then area (ΔADO) = area (ΔCDO)
Then; area (ΔBAO) area (ΔBCO) ......(1)
In a ΔPAC, Since PO is a median
Then, area (ΔPAO) = area (ΔPCO) ......(2)
⇒ Area (ΔABP) = Area of ΔCBP
APPEARS IN
संबंधित प्रश्न
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in
area. If G is the mid-point of median AD, prove that ar (Δ BGC) = 2 ar (Δ AGC).
PQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB || QR. If area of ΔPBQ is 17cm2, find the area of ΔASR.
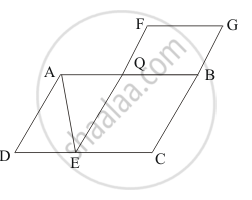
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
Find the area of a square, whose side is: 4.1 cm.
What will happen to the area of a rectangle, if its length and breadth both are trebled?
By counting squares, estimate the area of the figure.

Is the area of your belt the same as the area of the postcard? Why or why not?
Whose footprint is larger - yours or your friend’s?
How will you decide? Discuss.
Find the area of the following figure by counting squares:

