Advertisements
Advertisements
प्रश्न
A point D is taken on the side BC of a ΔABC such that BD = 2DC. Prove that ar(Δ ABD) =
2ar (ΔADC).
उत्तर
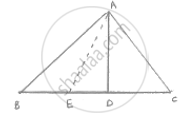
GIven that ,
In ΔABC, BD = 2 DC
To prove: ar ( ΔABD ) = 2ar (ΔADC)
Construction: Take a point E on BD such that BE = ED
Proof : Since, BE = ED and 2 BD = 2DC
Then, BE = ED = DC
We know that median of Δledivides it into two equal Δles
∴ In , ΔABD , AE is a median
Then, area (ΔABD) 2ar (ΔAED) .....(1)
In , ΔAEC , AD is a median
Then area (ΔAED) = area (ΔADC) ...... (2)
Compare equation (1) and (2)
Area (ΔABD) = 2ar (ΔADC).
APPEARS IN
संबंधित प्रश्न
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
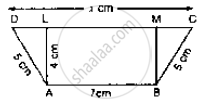
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
In the given figure, find the area of ΔGEF.
If AD is median of ΔABC and P is a point on AC such that
ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (Δ PDC) : ar (Δ ABC)
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
Find the area of a rectangle whose length = 24 cm breadth =180 mm
Find the area of a square, whose side is: 4.5 cm.
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

