Advertisements
Advertisements
рдкреНрд░рд╢реНрди
If ABCD is a parallelogram, then prove that
ЁЭСОЁЭСЯ (ΔЁЭР┤ЁЭР╡ЁЭР╖) = ЁЭСОЁЭСЯ (ΔЁЭР╡ЁЭР╢ЁЭР╖) = ЁЭСОЁЭСЯ (ΔЁЭР┤ЁЭР╡ЁЭР╢) = ЁЭСОЁЭСЯ (ΔЁЭР┤ЁЭР╢ЁЭР╖) = `1/2` ЁЭСОЁЭСЯ (||ЁЭСФЁЭСЪ ЁЭР┤ЁЭР╡ЁЭР╢ЁЭР╖) .
Advertisements
рдЙрддреНрддрд░
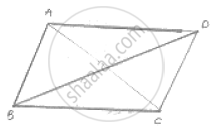
Given: ABCDis a parallelogram
To prove : area (ΔЁЭР┤ЁЭР╡ЁЭР╖) = ЁЭСОЁЭСЯ (ΔAЁЭР╡ЁЭР╢) = are (Δ ACD)
= `1/2` ЁЭСОЁЭСЯ (||ЁЭСФЁЭСЪ ЁЭР┤ЁЭР╡ЁЭР╢ЁЭР╖)
Proof: we know that diagonals of a parallelogram divides it into two equilaterals.
Since, AC is the diagonal.
Then, ЁЭСОЁЭСЯ (ΔЁЭР┤ЁЭР╡ЁЭР╢) = (Δ ACD) = `1/2` ЁЭСОЁЭСЯ (||ЁЭСФЁЭСЪ ЁЭР┤ЁЭР╡ЁЭР╢ЁЭР╖)............ (1)
Since, BD is the diagonal
Then, ЁЭСОЁЭСЯ (ΔЁЭР┤ЁЭР╡ЁЭР╢) = ЁЭСОЁЭСЯ (ΔЁЭР╡ЁЭР╢ЁЭР╖) = `1/2` ЁЭСОЁЭСЯ (||ЁЭСФЁЭСЪ ЁЭР┤ЁЭР╡ЁЭР╢ЁЭР╖)............ (2)
Compare equation (1) and (2)
∴ ЁЭСОЁЭСЯ (ΔЁЭР┤ЁЭР╡ЁЭР╢) = ЁЭСОЁЭСЯ (ΔЁЭР┤ЁЭР╢ЁЭР╖)
= ЁЭСОЁЭСЯ (ΔЁЭР┤ЁЭР╡ЁЭР╖) = ЁЭСОЁЭСЯ (ΔЁЭР╡ЁЭР╢ЁЭР╖) = `1/2` ЁЭСОЁЭСЯ (||ЁЭСФЁЭСЪ ЁЭР┤ЁЭР╡ЁЭР╢ЁЭР╖)
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
Compute the area of trapezium PQRS is Fig. below.
In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If
OE = 2√5, find the area of the rectangle.
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove
that: (1) ar (ΔADO) = ar (ΔCDO) (2) ar (ΔABP) = ar (ΔCBP)
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC) : ar (ΔBDE).
The median of a triangle divides it into two ______.
If AD is median of ΔABC and P is a point on AC such that
ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (Δ PDC) : ar (Δ ABC)
Find the area and perimeter of the following parallelograms
Measure the length of the floor of your classroom in meters. Also measure the width.
- If you want to move around easily then how many children do you think should be there in one square meter?
Find the area of the following figure by counting squares:
