Advertisements
Advertisements
प्रश्न
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
उत्तर
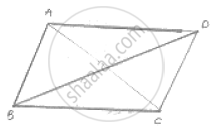
Given: ABCDis a parallelogram
To prove : area (Δ𝐴𝐵𝐷) = 𝑎𝑟 (ΔA𝐵𝐶) = are (Δ ACD)
= `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷)
Proof: we know that diagonals of a parallelogram divides it into two equilaterals.
Since, AC is the diagonal.
Then, 𝑎𝑟 (Δ𝐴𝐵𝐶) = (Δ ACD) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷)............ (1)
Since, BD is the diagonal
Then, 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷)............ (2)
Compare equation (1) and (2)
∴ 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷)
= 𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷)
APPEARS IN
संबंधित प्रश्न
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
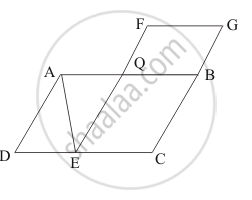
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
Find the area of a rectangle whose length = 8.5 m breadth = 5 m.
Find the area and perimeter of the following parallelograms
Is the area of your belt the same as the area of the postcard? Why or why not?
If each square on this page is equal to 1 square meter of land, how much land will each of her children get? ________ square m
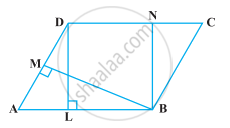
In the following figure, the area of parallelogram ABCD is ______.
An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
Find the area of the following figure by counting squares:

