Advertisements
Advertisements
प्रश्न
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
विकल्प
12 sq. units
6 sq. units
4 sq. units
3 sq. units
उत्तर
Given: (1) The Area of ΔABC = 24 sq units.
(2) ΔPQR is formed by joining the midpoints of ΔABC
To find: The area of ΔPQR
Calculation: In ΔABC, we have
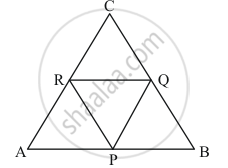
Since Q and R are the midpoints of BC and AC respectively.
∴ PQ || BA ⇒ PQ || BP
Similarly, RQ || BP. So BQRP is a parallelogram.
Similarly APRQ and PQCR are parallelograms.
We know that diagonal of a parallelogram bisect the parallelogram into two triangles of equal area.
Now, PR is a diagonal of ||gmAPQR.
∴ Area of ΔAPR = Area of ΔPQR ……(1)
Similarly,
PQ is a diagonal of ||gm PBQR
∴ Area of ΔPQR = Area of ΔPBQ ……(2)
QR is the diagonal of ||gm PQCR
∴ Area of ΔPQR = Area of ΔRCQ ……(3)
From (1), (2), (3) we have
Area of ΔAPR = Area of ΔPQR = Area of ΔPBQ = Area of ΔRCQ
But
Area of ΔAPR + Area of ΔPQR + Area of ΔPBQ + Area of ΔRCQ = Area of ΔABC
4(Area of ΔPBQ) = Area of ΔABC
`= 1/4 `Area of ΔABC
∴ Area of ΔPBQ `= 1/4 (24)`
= 6 sq units
APPEARS IN
संबंधित प्रश्न
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in
area. If G is the mid-point of median AD, prove that ar (Δ BGC) = 2 ar (Δ AGC).
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC) : ar (ΔBDE).
ABCD is a trapezium in which AB || DC. If ar (ΔABD) = 24 cm2 and AB = 8 cm, then height of ΔABC is
Find the area of a rectangle whose length = 24 cm breadth =180 mm
Find the area and perimeter of the following parallelograms
The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| 13 cm | ? | 54 cm | ? |
Is the area of the blue shape more than the area of the yellow shape? Why?

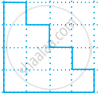
The region given in the following figure is measured by taking  as a unit. What is the area of the region?
as a unit. What is the area of the region?
Find the area of the following figure by counting squares: