Advertisements
Advertisements
प्रश्न
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
पर्याय
12 sq. units
6 sq. units
4 sq. units
3 sq. units
उत्तर
Given: (1) The Area of ΔABC = 24 sq units.
(2) ΔPQR is formed by joining the midpoints of ΔABC
To find: The area of ΔPQR
Calculation: In ΔABC, we have
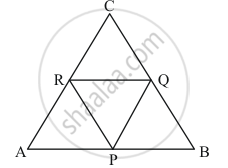
Since Q and R are the midpoints of BC and AC respectively.
∴ PQ || BA ⇒ PQ || BP
Similarly, RQ || BP. So BQRP is a parallelogram.
Similarly APRQ and PQCR are parallelograms.
We know that diagonal of a parallelogram bisect the parallelogram into two triangles of equal area.
Now, PR is a diagonal of ||gmAPQR.
∴ Area of ΔAPR = Area of ΔPQR ……(1)
Similarly,
PQ is a diagonal of ||gm PBQR
∴ Area of ΔPQR = Area of ΔPBQ ……(2)
QR is the diagonal of ||gm PQCR
∴ Area of ΔPQR = Area of ΔRCQ ……(3)
From (1), (2), (3) we have
Area of ΔAPR = Area of ΔPQR = Area of ΔPBQ = Area of ΔRCQ
But
Area of ΔAPR + Area of ΔPQR + Area of ΔPBQ + Area of ΔRCQ = Area of ΔABC
4(Area of ΔPBQ) = Area of ΔABC
`= 1/4 `Area of ΔABC
∴ Area of ΔPBQ `= 1/4 (24)`
= 6 sq units
APPEARS IN
संबंधित प्रश्न
If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove
that ar (Δ PQE) = ar (ΔCFD).
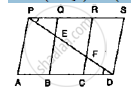
In the given figure, find the area of ΔGEF.
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
By counting squares, estimate the area of the figure.

By counting squares, estimate the area of the figure.

Find the area and perimeter of the following parallelograms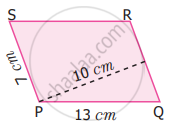
The region given in the following figure is measured by taking  as a unit. What is the area of the region?
as a unit. What is the area of the region?
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

